Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A , n ( Ω ) la số phân tử của không gian mẫu.
+ Chú ý rằng: Nếu số được lấy ra có chữ số đứng trước nhỏ hơn chữ số đứng sau thì không thể có số 0 trong số đó.
Cách giải: + Số có 6 chữ số khác nhau là a b c d e f với a , b , c , d , e , f ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9
Nên a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 7 cách chọn, e có 6 cách chọn và f có 5 cách chọn.Suy ra số phần tử của không gian mẫu n Ω = 9 . 9 . 8 . 7 . 6 . 5 = 136080
+ Gọi A là biến cố a b c d e f là số lẻ và a < b < c < d < e < f
Suy ra không thể có chữ số 0 trong số a b c d e f và f ∈ 7 ; 9 .
+ Nếu f = 7 ⇒ a , b , c , d , e ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 mà với mỗi bộ 5 số được lấy ra ta chỉ ó duy nhất 1 cách sắp xếp theo thứ tự tăng dần nên có thể lập được C 6 5 = 6 số thỏa mãn.
+ Nếu f = 9 ⇒ a , b , c , d , e ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 mà với mỗi bộ 5 số được lấy ra ta chỉ ó duy nhất 1 cách sắp xếp theo thứ tự tăng dần nên có thể lập được C 8 5 = 56 số thỏa mãn.
Suy ra n A = 6 + 56 = 62 nên xác suất cần tìm là P A = n A n Ω = 62 136080 = 31 68040

Số có 5 chữ số khác nhau sắp xếp theo chiều tăng dần từ tập số 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 là: . C 7 5
Số có 5 chữ số khác nhau sắp xếp theo chiều tăng dần từ tập số 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 có a = 0 là: 1 C 6 4 = C 6 4 .
Vậy số các chữ số cần tìm theo yêu cầu của đề bài là: C 7 5 - C 6 4 .
Chọn B.

Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
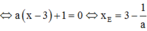
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó 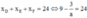
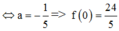

Đáp án A
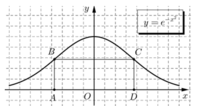
Theo hình vẽ , gọi D t ; 0 , A − t ; 0 và C t ; e − t 2 , B − t ; e − t 2 với t>0
Suy ra A B ¯ = 0 ; e − t 2 ⇒ A B = e − t 2 và B C = 2 t → S A B C D = A B . B C = 2 t . e − t 2
Xét hàm số f t = t e t 2 trên khoảng 0 ; + ∞ , có f ' t = 1 − 2 t 2 e − t 2
Do đó, giá trị lớn nhất của hàm số f t là max 0 ; + ∞ f t = 1 2 e . Vậy S max = 2 e

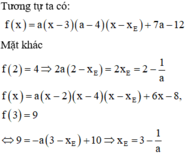
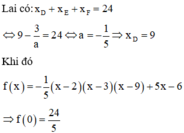
ABCD = 2178
E = 4
DCBA: 8712
8712