Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)

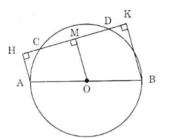
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)

BAN TU VE HINH NHA
tu O ke OI vuong goc vs CD \(\Rightarrow CI=ID\)
de dang cm dc AH song song vs IO song song vs KB (cung vuong goc vs CD)
suy ra AHKB la hinh thang
lai co OA=OB \(\Rightarrow IH=IK\)
\(\Rightarrow IH-CI=IK-ID\Rightarrow CH=BK\)
Kẻ \(OM\perp CD\)
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB ( bán kính )
OM // AH // BK ( cùng vuông góc HK )
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK (đpcm)

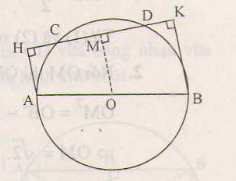
Vẽ ta được CM=DM. (1)
Ta có OM // AH //BK (cùng vuông góc với CD).
Mặt khác , OA=OB nên MH=MK. (2)
Từ (1) và (2) suy ra CH=DK.
Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.

VẽOM⊥CDta được CM=DM. (1)
Ta có OM // AH //BK (cùng vuông góc với CD).
Mặt khác , OA=OB nên MH=MK. (2)
Từ (1) và (2) suy ra CH=DK.
Nhận xét. Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau.

a: Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ACB}=90^0\)
b: Xét (O) có
OH là một phần đường kính
CD là dây
OH\(\perp\)CD tại H
Do đó: H là trung điểm của CD
Xét tứ giác ECAD có
H là trung điểm của đường chéo CD
H là trung điểm của đường chéo EA
Do đó: ECAD là hình bình hành
mà EA\(\perp\)CD
nên ECAD là hình thoi