Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

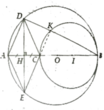
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0

Bài 1 thiếu đề
Bài 2 Mình không vẽ được hình nên bạn thông cảm
Xét tam giác vuông ACO có \(CM\perp AO\)
=> \(OM.OA=OC^2=OD^2\)
=> \(\frac{OD}{OA}=\frac{OM}{OD}\)
=> tam giác MDO đồng dạng tam giác DAO
=> MDO=OAD
Mà MDO=DEO
=> OAD=DEO
=> tứ giác ADOE nội tiếp
Vậy tứ giác ADOE nội tiếp
Gọi I là tâm đường tròn đường kính CB
a) Xét (O) có: \(\widehat{ADB}\) \(=90^0\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\perp DB\)
Xét (I) có: \(\widehat{CKB}\) \(=90^0\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow CK\perp KB\) hay \(CK\perp DB\)
Ta có: \(\widehat{DKC}+\widehat{CKB}\) \(=180^0\) (hai góc kề bù)
\(\Leftrightarrow\) \(\widehat{DKC}\) \(=180^0-\) \(\widehat{CKB}\) \(=180^0-90^0=90^0\)
Vì \(\widehat{ADB}+\widehat{DKC}\) \(=90^0+90^0=180^0\)
\(\Rightarrow\) Tứ giác DKCH nội tiếp đường tròn (theo dhnb tứ giác nội tiếp)
b) Vì H là trung điểm AC
\(\Rightarrow AH=HC\)
Xét (O) có: \(\left\{{}\begin{matrix}AB=2R\\DE\perp AB=\left\{H\right\}\end{matrix}\right.\)
\(\Rightarrow DH=HE\) (liên hệ giữa đường kính và dây)
Xét tứ giác ADCE có: \(\left\{{}\begin{matrix}DH=HE\\AH=HC\\DE\cap AC=\left\{H\right\}\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác ADCE là hình bình hành (theo dhnb hình bình hành)
(mà \(DE\perp AC=\left\{H\right\}\))
\(\Rightarrow\) Hình bình hành ADCE là hình thoi (theo dhnb hình thoi)
\(\Rightarrow\) AD//EC (1)
Vì \(\left\{{}\begin{matrix}AD\perp DB\\CK\perp DB\end{matrix}\right.\) \(\Rightarrow\) AD//CK (từ vuông góc đến song song) (2)
Từ (1) và (2) \(\Rightarrow\) AD//EC//CK
\(\Rightarrow\) E,C,K thẳng hàng.
c) Vì \(DE\perp AC=\left\{H\right\}\)
\(\Rightarrow\) \(\widehat{DHA}\) \(=90^0\)
Vì AD//EC \(\Rightarrow\) \(\widehat{ACE}=\widehat{DAC}\) hay \(\widehat{DAH}=\widehat{HCE}\)
(mà \(\widehat{HCE}=\widehat{KCB}\) vì hai góc đối đỉnh)
\(\Rightarrow\) \(\widehat{DAH}=\widehat{KCB}\)
Xét ΔADH∼ΔCBK vì:
\(\widehat{DHA}=\widehat{CKB}\) \(=90^0\)
\(\widehat{DAH}=\widehat{KCB}\) (cmtrn)
\(\Rightarrow\frac{AD}{CB}=\frac{AH}{CK}\Leftrightarrow AD\cdot CK=AH\cdot CB\) (mà \(AH=HC\))
\(\Leftrightarrow AD\cdot CK=HC\cdot CB\) (đpcm)