Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Em tự giải
b.
Do \(AM||BN\) (cùng vuông góc AB) \(\Rightarrow\widehat{AMN}+\widehat{BNM}=180^0\) (2 góc trong cùng phía)
Mà \(\widehat{AMN}+\widehat{AIE}=180^0\) (AMEI nội tiếp) \(\Rightarrow\widehat{AIE}=\widehat{BNM}\) (1)
Lại có \(\widehat{NBE}=\widehat{BAE}\) (cùng phụ \(\widehat{ABE}\)) (2)
(1);(2) \(\Rightarrow\Delta IAE\sim\Delta NBE\left(g.g\right)\) (3)
\(\Rightarrow\dfrac{IE}{NE}=\dfrac{IA}{NB}\Rightarrow IA.NE=IE.NB\)
\(\Rightarrow\dfrac{1}{3}IB.NE=IE.NB\Rightarrow IB.NE=3IE.NB\)
c.
AMEI nội tiếp \(\Rightarrow\widehat{AMI}=\widehat{AEI}\) (cùng chắn AI)
Từ (3) \(\Rightarrow\widehat{AEI}=\widehat{NEB}\) \(\Rightarrow\widehat{AMI}=\widehat{NEB}\)
Lại có tứ giác BNEI nội tiếp (B và E đều nhìn IN dưới 1 góc vuông)
\(\Rightarrow\widehat{NEB}=\widehat{NIB}\) (cùng chắn NB)
\(\Rightarrow\widehat{AMI}=\widehat{NIB}\)
\(\Rightarrow\Delta_VAMI\sim\Delta_VBIN\left(g.g\right)\)
\(\Rightarrow\dfrac{AM}{BI}=\dfrac{AI}{BN}\Rightarrow AM.BN=AI.BI=\dfrac{R}{2}.\dfrac{3R}{2}=\dfrac{3R^2}{4}\)
Đặt \(AM=x>0\Rightarrow BN=\dfrac{3R^2}{4x}\)
Ta có: \(S_{MIN}=S_{ABNM}-\left(S_{AMI}+S_{BIN}\right)=\dfrac{\left(AM+BN\right).AB}{2}-\left(\dfrac{AM.AI}{2}+\dfrac{BN.BI}{2}\right)\)
\(=\dfrac{\left(x+\dfrac{3R^2}{4x}\right).2R}{2}-\left(\dfrac{x.\dfrac{R}{2}}{2}+\dfrac{\dfrac{3R^2}{4x}.\dfrac{3R}{2}}{2}\right)\)
\(=\dfrac{3Rx}{4}+\dfrac{3R^3}{16x}=\dfrac{3R}{4}\left(x+\dfrac{R^2}{4x}\right)\ge\dfrac{3R}{4}.2\sqrt{\dfrac{R^2x}{4x}}=\dfrac{3R^2}{4}\)
Dấu "=" xảy ra khi \(x=\dfrac{R}{2}\) hay \(AM=AI\)

a: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
b: góc IEN+góc IBN=180 độ
=>IENB nội tiếp
=>góc ENI=góc EBI
góc MIN=góc MIE+góc NIE
=góc MAE+góc NBE
=90 độ-góc EAI+90 độ-góc EBI=90 độ

1: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
2: góc IEN+góc IBN=180 độ
=>IENB nội tiếp
MAIE nội tiếp
=>góc AMI=góc AEI
IENB nội tiếp
=>góc BIN=góc BEN
góc BEN+góc IEB=90 độ
góc AEI+góc BEI=90 độ
=>góc BEN=góc AEI
=>góc AMI=góc BIN

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')
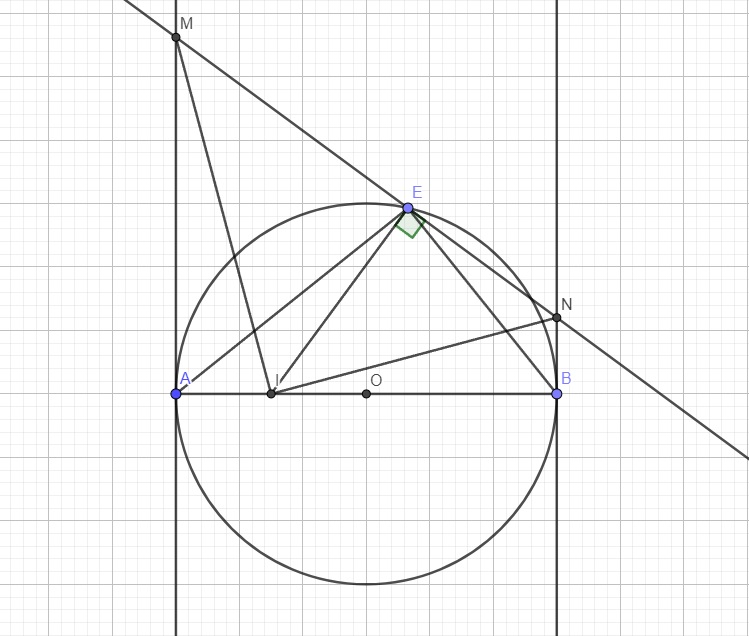
a: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
b: AMEI nội tiếp
=>góc EAI=góc EMI=góc EIN
IENB nội tiếp
=>góc EIN=góc EBN
=>góc EAI=góc EBN
IENB nội tiếp
=>góc AIE=góc BNE
=>ΔAIE đồng dạng vơi ΔBNE
=>AI*NE=IE*NB
=>IB*NE=3*IE*NB