Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
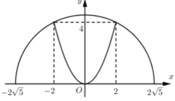
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 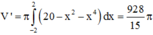
=> Thể tích cần tính 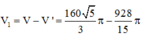
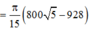

1: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Ta có: CM+MD=CD
nên CD=AC+BD
2: Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
3: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
hay \(AC\cdot BD=\left(\dfrac{AB}{2}\right)^2=\dfrac{AB^2}{4}\)
4: Ta có: CM=CA
nên C nằm trên đường trung trực của MA(3)
Ta có: OM=OA
nên O nằm trên đường trung trực của MA(4)
Từ (3) và (4) suy ra OC\(\perp\)MA(5)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
Suy ra: MA\(\perp\)MB(6)
Từ (5) và (6) suy ra MB//OC

a)xét tam giác BCE và tam giác DCE có:
\(\widehat{DBE}=\widehat{BCE}=90^o\)
\(\widehat{BEC}:chung\)
nên tam giác BCE ~ tam giác DBE(g-g)