Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có: E C A ^ + O C A ^ = 90 0 và A C H ^ + O A C ^ = 90 0
mà O A C ^ = O C A ^ (do tam giác AOC cân tại O)
Suy ra E C A ^ = A C H ^
Khi đó E A C ^ = H A C ^ (cùng lần lượt phụ với E C A ^ và A C H ^ ), ta có đpcm
b, Chứng minh tương tự suy ra BC là phân giác của F B H ^
Từ đó, chứng minh được BC vuông góc HF (1)
Tam giác ABC có trung tuyến OC = 1 2 AB. Suy ra tam giác ABC vuông tại C , tức là BC vuông góc với AC (2)
Từ (1),(2) suy ra đpcm
c, Ta có : AE+BF =2OC=2R không đổi
d, Ta có A E . B F ≤ A E + B F 2 4 = R 2
suy ra AE.BF lớn nhất = R 2 óAE=BF=R
Điều này xẩy ra khi C là điểm chính giữa cung AB

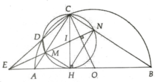
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm
a: Xét tứ giác MEAH có
góc MEA+góc MHA=180 độ
=>MEAH là tứ giác nội tiếp
b: ME//AO
=>góc EMA=góc OAM=góc OMA
=>MA là phân giác của góc EMO
MEAH là tứgiác nội tiếp
=>goc EHF=góc EMA
FAHN là tứ giác nội tiếp
=>góc FHA=góc FNA
góc FHA+góc EHF=góc EMA+góc FNA=90 độ
=>góc EHF=90 độ
Ko có câu c à bn