Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
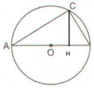
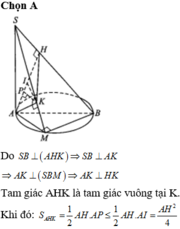
Quay tam giác AHC quanh trục AB thu được hình nón có h = AH; r = CH.



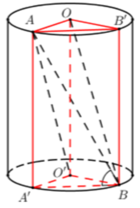
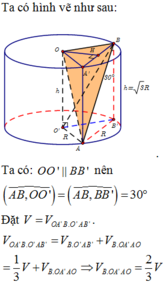
Lấy điểm A ' ∈ O ' ; B ' ∈ O sao cho A A ' ; B B ' song song với trục O O ' .
Khi đó ta có lăng trụ đứng O A B ' . O ' A ' B .
Ta có:
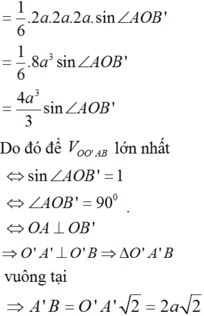
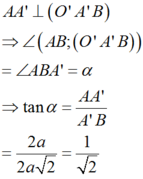
Chọn A.

Đáp án B
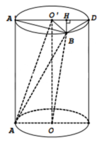
Kẻ đường sinh AA’, gọi D là điểm đối xứng A’ qua tâm O’.
Kẻ BH vuông góc với A ' D ⇒ B H ⊥ A O O ' A ' ⇒ V O O ' A B = 1 3 . B H . S Δ O O ' A
Mà S Δ O O ' A = 1 2 . O O ' . O A = 2 a 2 ⇒ V O O ' A B = 2 a 2 3 x B H
Để V O O ' A B lớn nhất ⇔ B H = B O ' H ≡ O ' ⇒ A ' B = 2 a 2
Tam giác AA’B vuông tại A’, có tan A B A ' ^ = A A ' A ' B = 2 a 2 a 2 = 1 2
Vậy A B ; O ' ^ = A B ; A ' B ^ = A B A ' ^ = α ⇒ tan α = 1 2


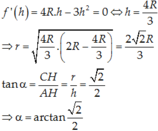




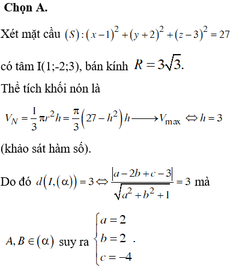
Đáp án C
Phương pháp:
- Tính thể tích khối nón có được khi quay tam giác ACH quanh AB (hay AH) bằng công thức V = 1 3 S d . h với đáy là hình tròn tâm H bán kính CH và chiều cao là AH.
- Tìm GTLN của thể tích dựa vào phương pháp xét hàm, từ đó tìm được AH.
Cách giải: Thể tích khối nón khi quay Δ A C H quay quanh AB:
V = 1 3 A H . π . C H 2 = 1 3 A H . π . A H . A B − A H 2 = 2 R π 3 . A H 2 − π 3 A H 3
Chú ý khi giải:
Ở bước kết luận nhiều HS sẽ kết luận sai góc α là góc 45 ° dẫn đến chọn sai đáp án.