Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
+) Khẳng định i): a > 2019 thì a x > 2019 x ∀ x ∈ ℝ ⇒ x = 1 khẳng định sai.
+) Khẳng định ii): a > 2019 thì b a > b 2019 ∀ b > 0 ⇔ b > 0 khẳng định sai.
+) Khẳng định iii): a > 2019 thì log b a > log b 2019 ∀ n > 0 ; b ≢ 0 ⇔ b > 1 khẳng định sai
Chọn A.

Xét khai triển
1 + x 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 x + C 2 n + 1 2 x 2 + C 2 n + 1 3 x 3 + C 2 n + 1 4 x 4 + . . . + C 2 n + 1 2 n + 1 x 2 n + 1
Lấy đạo hàm cả hai vế ta được
2 n + 1 x 2 n = C 2 n + 1 1 - 2 x C 2 n + 1 2 + 3 x 2 C 2 n + 1 3 - 4 x 3 . C 2 n + 1 4 + . . + 2 n + 1 x 2 n C 2 n + 1 2 n + 1
Thay x = -2 vào ta được
2 n + 1 x 2 n = C 2 n + 1 1 + 2 x . 2 . C 2 n + 1 2 + 3 x 2 C 2 n + 1 3 - 4 x 3 C 2 n + 1 4 + . . + 2 n + 1 x 2 n C 2 n + 1 2 n + 1
Kết hợp với giả thiết bài toán ta được: 2 n + 1 = 2019 ⇔ n = 2019
Vậy n = 1009 là giá trị cần tìm
Đáp án A

Chọn B
Cách giải: Ta có:
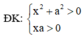
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
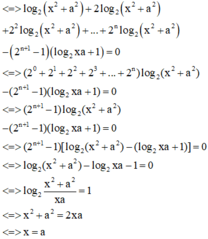
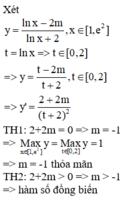
![]()
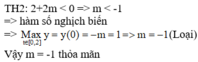
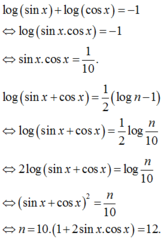
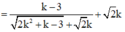

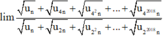
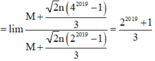 .
.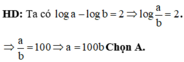
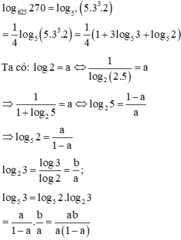
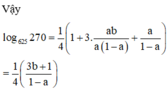
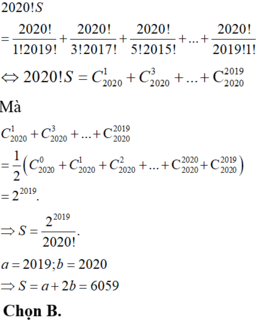
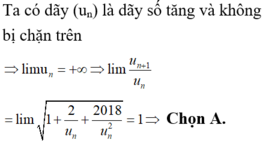
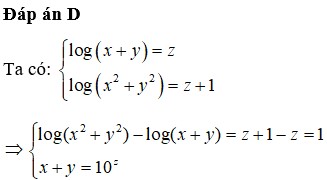
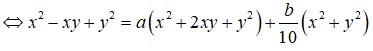
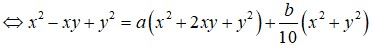
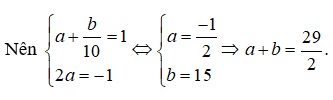
Đáp án A
Phương pháp:
Biến đổi VT để xuất hiện log a 2019
Sử dụng công thức 1 3 + 2 3 + 3 3 + ... + n 3 = n 2 n + 1 2 4
Cách giải:
Ta có:
V T = 1 2 . log a 2019 + 2 2 log a 2019 + ... n 2 . log a n 2019
Vậy. = 1 3 . log a 2019 + 2 3 log a 2019 + ... + n 3 . log a 2019
= 1 3 + 2 3 + ... + n 3 . log a 2019
V T = 1010 2 .2019 2 . log a 2019
Có V T = V P
⇔ 1 3 + 2 3 + ... + n 3 log a 2019 = 1010 2 .2019 2 . log a 2019
⇔ n 2 n + 1 2 4 = 1010 2 .2019 2
⇔ n 2 + n 2 = 2020.2019 2
⇔ n 2 + n = 2020.2019 vì n 2 + n > 0 , ∀ n > 0
⇔ n = 2019 ∈ 0 ; + ∞ n = − 2020 ∉ 0 ; + ∞
Vậy n = 2019
Chú ý khi giải:
HS thường không biết áp dụng công thức 1 3 + 2 3 + 3 3 + ... + n 3 = n 2 n + 1 2 4 dẫn đến không tìm ra kết quả bài toán.