Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

Lời giải:
$1440=2^5.3^2.5$
Để $k=n!\vdots 1440$ thì $n!\vdots 2^5$; $n!\vdots 3^2; n!\vdots 5$
Để $n!\vdots 3^2; 5$ thì $n\geq 6(1)$
Để $n!\vdots 2^5$. Để ý $2=2^1, 4=2^2, 6=2.3, 8=2^3$. Để $n!\vdots 2^5$ thì $n\geq 8(2)$
Từ $(1); (2)$ suy ra $n\geq 8$. Giá tri nhỏ nhất của $n$ có thể là $8$

Chọn A
Với số tự nhiên n ≥ 1, ta có:
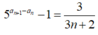
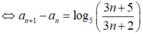
![]()
Suy ra:
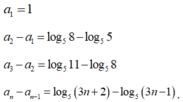
Cộng tương ứng hai vế các đẳng thức trên ta có ![]() với mọi số tự nhiên n
≥
1
với mọi số tự nhiên n
≥
1
Để ![]()
![]()
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
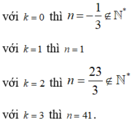
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
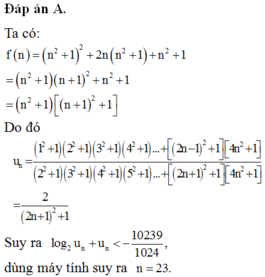
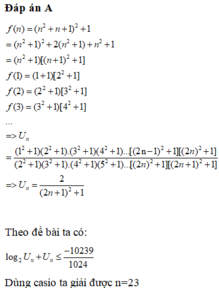

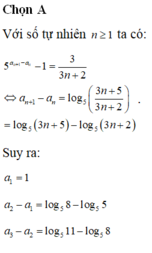




Chọn A