Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
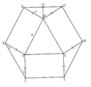
Ba đường thẳng d1, d2, d3 cắt nhau tại ba điểm A, B, C chia ngũ giác thành bảy phần với các diện tích được ký hiệu như trên hình
Ta thấy:
S3 + S2 + S7 = \(\dfrac{1}{2}\)S
= S1 + S2 + S7 + S6
S3 = S1 + S6 (1)
Ta cũng có:
\(\dfrac{1}{2}\)S = S1 + S2 + S3 + S4 (2)
Thay (1) vào (2) ta được:
\(\dfrac{1}{2}\)S = 2S1 + S2 + S3 + S4 + S6 > 2S1
Tức là S1 < \(\dfrac{1}{4}\)S

xét hình ngũ giác ta thấy có tất cả là 5 đường chéo mà theo như đề bài đã cho thì mỗi đường chéo cắt ra khỏi một tam giác có diện tích bằng 1.
=> có tất cả 5 hình tam giác được cắt ra.
diện tích hình ngũ giác:
S=S1+S2+S3+S4+S5=1+1+1+1+1=5
( S1...5là tam giác 1.....tam giác 5 0

Số đo mỗi góc của ngũ giác đều là 1080.
Ta có tam giác ABC cân tại B
⇒ A 1 ^ = C 1 ^ = ( 180 0 − 108 0 ) : 2 = 36 0 ⇒ E A C ^ = D C A ^ (1)
Chứng minh tương tự ta được:
C 3 ^ = E ^ 1 = 36 0 ⇒ C 2 ^ = 36 0
Có C 2 ^ = E 1 ^ = 36 0 ⇒ E D / / A C (2)
Từ (1) và (2), suy ra ACDE là hình thang cân (ĐPCM)
(Các khác: Có thể chứng minh hình thang ACDE có hai đường chéo bằng nhau)
* Chứng minh tương tự ta có J E F ^ = E F G ^ = F G H ^ = G H I ^ = H I J ^ = I J E ^ .
Vậy tứ giác CDEK là hình bình hành
mà CD = DE, suy ra hình bình hành CDEK là hình thoi (ĐPCM)