Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.

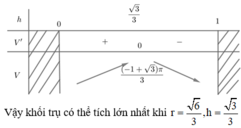

Đáp án A
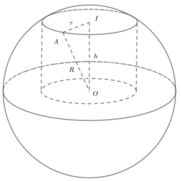
Vì hình trụ nội tiếp trong mặt cầu bán kính R cố định
⇒ R 2 = r 2 + h 2 2 = r 2 + h 2 4 ≥ 2 r 2 × h 2 4 = r h ⇒ r h = R 2
Diện tích xung quanh của hình trụ là: S x q = 2 πrh ≤ 2 πR 2
Dấu “=” xảy ra khi r 2 + h 2 4 = R 2 r 2 = h 2 4 ⇒ h = R 2 .

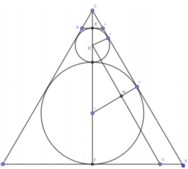
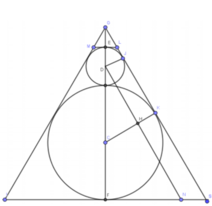
Gọi tâm của hai đường tròn trong (N) là C và D. Ta có GS là tiếp tuyến chung của hai đường tròn tại K và J. Khi đó: D J ⊥ G S C K ⊥ G S
Kẻ D N / / G S ( N ∈ I S ) , khi đó DHKJ là hình chữ nhật nên HK=DJ=1 cm, do đó ta có CH=2 cm.
Ta có ∆ D H C đồng dạng ∆ G J D nên D J C H = G D C D
⇒ D G = D J . C D C H = 1 . 4 2 = 2 cm từ đó suy ra GF = 9 cm.
Ta có ∆ D H C đồng dạng ∆ G F S ⇒ G S D C = G F D H
⇒ G S = D C . G F D H = D C . G F D C 2 - C H 2 = 6 3 cm
⇒ F S = G S 2 - G F 2 = 3 3 cm.
Vì ∆ G E L đồng dạng ∆ G F S nên E L F S = G E G F
⇒ E L = G E . F S G F = 1 . 3 3 9 = 3 3
Vì (N) là khói nón cụt nên:
V N = 1 3 E L 2 + F S 2 + E L . F S E F = 728 π 9
Chọn đáp án D.

Đáp án B
Mặt cầu tâm I(1;4;1) tiếp xúc với mặt phẳng (P) nên R = d I ; P = x 1 + 2 y 1 - 2 z 1 + 2 1 2 + 2 2 + - 2 2 = 3 .
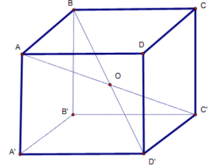

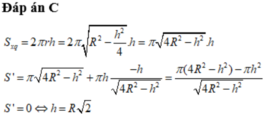
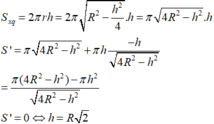

Đáp án A
Ta có: R 1 = I A , R 2 = I O , R 3 = I K . Mà I A > I K > I O nên R 1 > R 3 > R 2 .