Question

[Sam Sam]

Cho một cuộn cảm thuần L và hai tụ điện C1, C2 với C1>C2. Khi majhc dao động gồm cuộn cảm với C1 và C2 mắc nối tiếp thì tần số dao động của mạch là 50MHz, khi mạch gồm cuộn cảm với C1 mắc song song C2 thì tần số dao động của mạch là 24MHz. Khi mạch dao động gồm cuộn cảm với C1 thì tần số dao động của mạch là?

A. 25MHz

B. 35MHz

C. 30MHz

D. 40MHz

Answer 1

[Cao ngọc vũ]

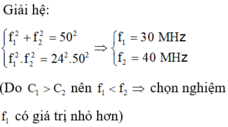
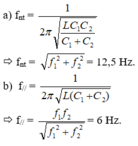
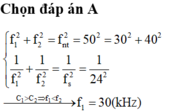
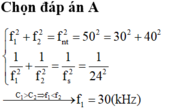
\(f=\frac{1}{2\pi\sqrt{LC}}\)

khi mắc nối tiếp thì \(C=\frac{C_1C_2}{C_1+C_2}\)

khi mắc song song thì \(C'=C_1+C_2\)

Ta có \(\frac{f}{f'}=\sqrt{\frac{C'}{C}}=\frac{25}{12}\Rightarrow\frac{C}{C'}=\frac{625}{144}\)

\(\Leftrightarrow144\left(C_1+C_2\right)=625\frac{C_1C_2}{C_1+C_2}\)

\(\Leftrightarrow144C_1^2-337C_1C_2+144C^2_2=0\)

\(\Leftrightarrow\left(16C_1-9C_2\right)\left(9C_1-16C_2\right)=0\)

do \(C_1>C_2\Rightarrow C_1=\frac{16}{9}C_2\Leftrightarrow C_2=\frac{9}{16}C_1\)

Ta có \(f'=\frac{1}{2\pi\sqrt{L\left(C_1+C_2\right)}}=\frac{1}{2\pi\sqrt{LC_1\times\frac{25}{16}}}=24\)

\(\Rightarrow\frac{1}{2\pi\sqrt{LC_1}}\times\frac{4}{5}=24\Rightarrow\frac{1}{2\pi\sqrt{LC_1}}=30\)

hay f1=30 Hz CHỌN C

Answer 2

[Cao ngọc vũ]

dòng thứ 4 trên xuống là \(\frac{C'}{C}=\frac{625}{144}\) nhé, mình viết nhầm đó ^^!