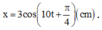Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Độ biến dạng của lò xo :![]()
Do vật dao động điều hòa nên phương trình dao động của vật có dạng :![]()
Với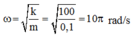
+ Theo bài ra tại t= 0 ![]()
![]()
![]()
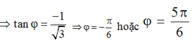
![]()
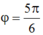
Thay vào (1) ta tìm được : A = 4 cm
![]()
Quảng đường vật đi được trong 1/3 chu kì kể từ thời điểm t = 0 là:
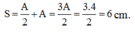

+ Ta có: Δ l = m g k = 1 cm
® Vị trí lò xo dãn 3 cm có: x = 2 cm
+ ω = k m = 10 10 rad/s
+ Áp dụng công thức độc lập ta được:
A = x 2 + v 2 ω 2 = 2 2 + 20 π 3 2 10 10 2 = 4 cm
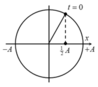
+ Dựa vào đường tròn ta xác định được vị trí t = 0
+ Từ t = 0 đi trong T 3 tương ứng với góc quét là φ = ω t = 2 π T . T 3 = 2 π 3
Tương ứng trên đường tròn là đi tới điểm A.
® S = A + A 2 = 6 cm
ĐÁP ÁN A

a) Từ định luật bảo toàn cơ năng ta có:
\(\frac{1}{2}mv^2_0=\frac{1}{2}kA^2\)
\(\Rightarrow A=v_0\sqrt{\frac{m}{k}}=2\sqrt{\frac{1}{1600}}=0,05m=5cm\)
b) Phương trình dao động có dạng: \(x=A\cos\left(\omega t+\varphi\right)\)
Tần số góc: \(\omega=\sqrt{\frac{k}{m}}=\frac{1600}{1}=40rad\text{/s }\)
Tại \(t=0\)\(\begin{cases}x=0=A\cos\varphi\\v=-2=-\omega A\sin\varphi\end{cases}\)\(\Rightarrow\varphi=\frac{\pi}{2}\)
Phương trình dao động: \(x=5\cos\left(40t+\frac{\pi}{2}\right)\left(cm\right)\)

Đáp án A
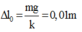
Ta có: ![]()
Quảng đường vật đi được trong một phần ba chu kì kể từ thời điểm ban đầu t= 0 là :
![]()

Độ giãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0\)
\(\Rightarrow \omega=\sqrt{\dfrac{g}{\Delta\ell_0}}\)
\(\Rightarrow \Delta\ell_0=\dfrac{g}{\omega^2}=\dfrac{10}{10^2}=0,1m=10cm\)
v = 0 thì lò xo không biến dạng, lúc đó \(x=\Delta\ell_0=10cm\)
Suy ra vị trí đó là ở biên, ta có: \(A=10cm\)
Khi \(v=80cm/s\) ta có: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow x^2=10^2-\dfrac{80^2}{10^2}\)
\(\Rightarrow x = \pm6cm\)
Lực đàn hồi: \(F_{dh}=k.\Delta\ell=k.|\Delta\ell_0+x|=50.|0,1\pm 0,06|\)
Suy ra \(F_{dh}=8N\)
Hoặc \(F_{dh}=2N\)