Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ số công suất của mạch khi điện áp hiệu dụng trên tụ hoặc cuộn cảm cực đại là
cos φ = 2 1 + ω C ω L − 1 ⇒ ω C ω L = 0 , 6
Kết hợp với Hz f 1 f 1 + 100 = 0 , 6 ⇒ f 1 = 150
Đáp án A

Hệ số công suất của mạch khi điện áp hiệu dụng trên tụ hoặc cuộn cảm cực đại là
cos φ = 2 1 + n P = P m a x cos 2 φ → cos 2 φ = 0 , 75 → n = 5 3
Kết hợp với n = f L f C ↔ 5 3 = f 1 + 100 f 1 → f 1 = 150 H z .
Đáp án A

Giải thích: Đáp án A
+ Khi C = C1 , ta có: điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U nên:
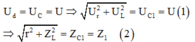
Điện áp toàn mạch khi đó:
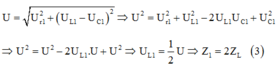
Thay vào (1), ta có: ![]()
Từ (2), (3), (4) ta có:
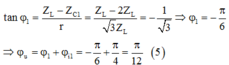
+ Khi C = C2 thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại nên
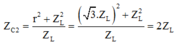
Tổng trở của mạch khi đó: ![]()
Độ lệch pha khi ZC = ZC2: 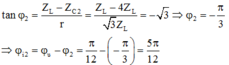
+ Áp dụng định luật Ôm cho cả hai trường hợp ta có:
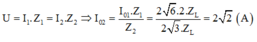
+ Biểu thức cường độ dòng điện khi ZC = ZC2:
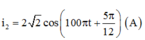

Chọn B
f = f1. → Zd = R 2 + Z L 1 2 =100Ω => R 2 + Z L 1 2 = 10 4
Khi UC = UCmax thì ZC1 = R 2 + Z L 1 2 Z L 1 => L C = R 2 + Z L 1 2 = 10 4 (*)
Khi f = f2; I = Imax trong mạch có cộng hưởng điện => ZC2 = ZL2
LC = 1 ω 2 2 = 1 4 π 2 f 2 2 (**)
Từ (*) và (**) => L2 = 10 4 4 π 2 f 2 2 => L = 10 2 2 πf 2 = 1 2 π = 0 , 5 π H

Đáp án B
+ Với φ 1 , φ 2 và φ 0 là độ lệch pha giữa u và I ứng với C 1 , C 2 , C 0
Ta có φ 1 + φ 2 = 2 φ 0 → φ 0 = - 52 , 5 0
+ Khi C C0 điện áp hiệu dụng trên tụ cực đại thì u R L vuông pha với u
+ Từ hình vẽ, ta có: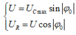
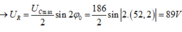
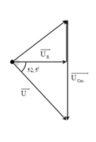

Đáp án B
+ Với φ 1 , φ 2 v à φ 0 là độ lệch pha giữa u và i ứng với C 1 , C 2 , C 0 . Ta có
φ 1 + φ 2 = 2 φ 0
→ φ 0 = - 52 , 5 0
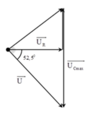
+ Khi C = C 0 điện áp hiệu dụng trên tụ cực đại thì u R L vuông pha với u.
+ Từ hình vẽ, ta có:
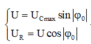
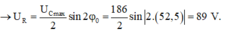

Đáp án B
+ Khi f = f1 điện áp hiệu dụng trên tụ là cực đại.
P = 0,75Pmax → 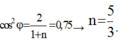 .
.
+ Khi f = f2 = f1 + 100 Hz, điện áp trên cuộn cảm là cực đại → 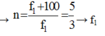 → f1 = 150 Hz
→ f1 = 150 Hz

Đáp án A
+ Khi C = C 2 mạch tiêu thụ công suất bằng 0,75 công suất cực đại
![]()
+ Biểu diễn lượng giác điện áp hiệu dụng trên tụ khi C thay đổi
![]()
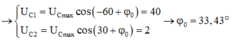
và U C m a x = 44 , 7 V
Kết hợp với
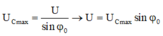
![]()
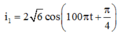
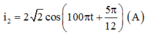
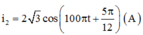
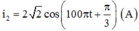
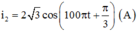

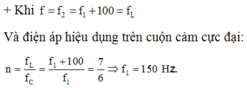
Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$
thầy có thể chứng minh cho e công thức liên quan tới Uc max không