Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(80+40\right)60}{80+40+60}=40\Omega\)
b. \(U=U12=U3=IR=40.0,15=6V\)(R12//R3)
\(\left\{{}\begin{matrix}I3=U3:R3=6:60=0,1A\\I12=I1=I2=U12:R12=6:\left(80+40\right)=0,05A\left(R1ntR2\right)\end{matrix}\right.\)

\(\text{Sơ đồ mạch: [R1 // (R4 nt R5)] nt (R2 // R3) nt R0 }\)
\(R_{4,5}=R_4+R_5=3\left(\text{Ω}\right)\)
\(R_{145}=\dfrac{R_1\cdot R_{45}}{R_1+R_{45}}=\dfrac{1\cdot3}{1+4}=0.75\left(\text{Ω}\right)\)
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{2\cdot6}{2+6}=1.5\left(\text{Ω}\right)\)
Điện trở tương đương của mạch là
\(R_{tđ}=R_0+R_{23}+R_{145}=0.5+1.5+0.75=2.75\left(\text{Ω}\right)\)

\(MCD:\left(R2//R3\right)ntR1\)
\(\rightarrow R=\dfrac{R2\cdot R3}{R2+R3}+R1=\dfrac{10\cdot12}{10+12}+10=\dfrac{170}{11}\Omega\)
\(I=I1=I23=U:R=24:\dfrac{170}{11}=\dfrac{132}{85}A\)
\(\rightarrow U1=I1\cdot R1=\dfrac{132}{85}\cdot10=\dfrac{264}{17}V\)
\(\rightarrow U23=U2=U3=U-U1=24-\dfrac{264}{17}=\dfrac{144}{17}V\)
\(\rightarrow\left\{{}\begin{matrix}I2=U2:R2=\dfrac{144}{17}:10=\dfrac{72}{85}A\\I3=U3:R3=\dfrac{144}{17}:12=\dfrac{12}{17}A\end{matrix}\right.\)
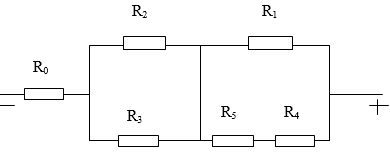
R2//(R1nt[R5//(R3ntR4))
\(=>R1345=R1+\dfrac{R5\left(R3+R4\right)}{R5+R3+R4}=7\Omega=>Rtd=\dfrac{R2.R1345}{R2+R1345}=14\Omega\)
\(=>I3=I4=I34=>U5=U34=I34.R34=0,5.\left(R3+R4\right)=3V=>I5=\dfrac{U5}{R5}=1A=>I1=I5+I34=1,5A=>U1345=U2=1,5.R1345=10,5V=U2=Um=>I2=\dfrac{U2}{R2}=1,5A\)
cái Rtd= 7x7/7+7 phải bằng 3.5Ω chứ sao lại=14Ω dc