Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(R_{12}=R_1+R_2=1+2=3\left(\Omega\right)\)
\(R_{tđ}=\dfrac{R_{12}.R_3}{R_{12}+R_3}=\dfrac{3.3}{3+3}=1,5\left(\Omega\right)\)
b) \(U=U_{12}=U_3=6V\)
\(I_{12}=I_1=I_2=\dfrac{U_{12}}{R_{12}}=\dfrac{6}{3}=2\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{6}{3}=2\left(A\right)\)
c) \(P=\dfrac{U^2}{R}=\dfrac{6^2}{1,5}=24\left(W\right)\)

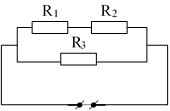
\(MCD:\left(R2//R3\right)ntR1\)
\(\rightarrow R=\dfrac{R2\cdot R3}{R2+R3}+R1=\dfrac{10\cdot12}{10+12}+10=\dfrac{170}{11}\Omega\)
\(I=I1=I23=U:R=24:\dfrac{170}{11}=\dfrac{132}{85}A\)
\(\rightarrow U1=I1\cdot R1=\dfrac{132}{85}\cdot10=\dfrac{264}{17}V\)
\(\rightarrow U23=U2=U3=U-U1=24-\dfrac{264}{17}=\dfrac{144}{17}V\)
\(\rightarrow\left\{{}\begin{matrix}I2=U2:R2=\dfrac{144}{17}:10=\dfrac{72}{85}A\\I3=U3:R3=\dfrac{144}{17}:12=\dfrac{12}{17}A\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)

Điện trở tương đương của mạch điện:
\(R_{tđ}=R_1+R_2+R_3=3+5+4=12\left(\Omega\right)\)
b, Đổi 500mA=0,5A
Hiệu điện thế giữa 2 đầu đoạn mạch
\(U=R_{tđ}\cdot I=12\cdot0,5=6\left(V\right)\)
c,Hiệu điện thế giữa hai đầu mỗi điện trở thành phần
\(I=I_1=I_2=I_3=0,5\left(A\right)\)
\(U_1=R_1I_1=3\cdot0,5=1,5\left(V\right)\)
\(U_2=R_2I_2=5\cdot0,5=2,5\left(V\right)\)
\(U_3=R_3I_3=4\cdot0,5=2\left(V\right)\)

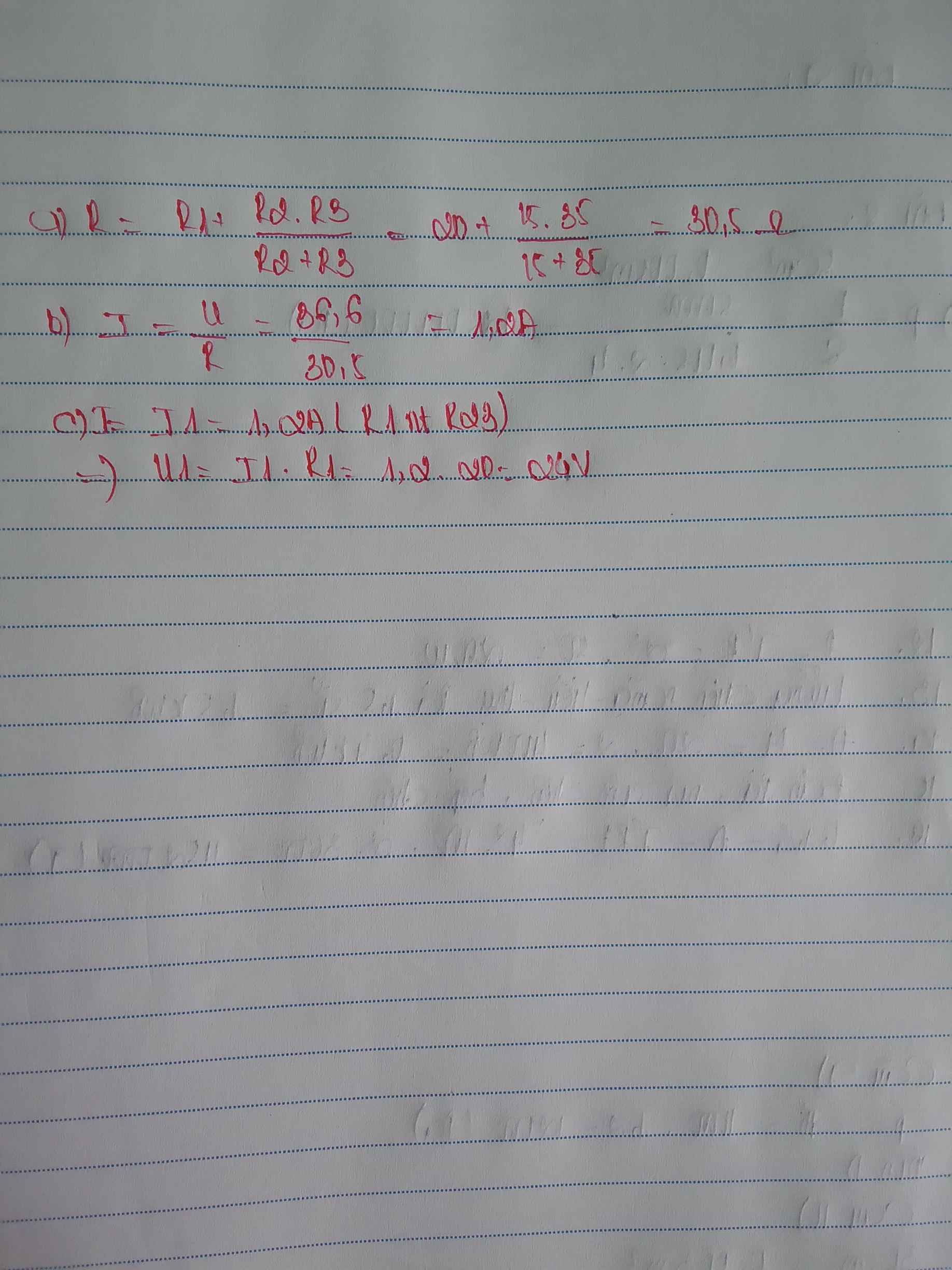
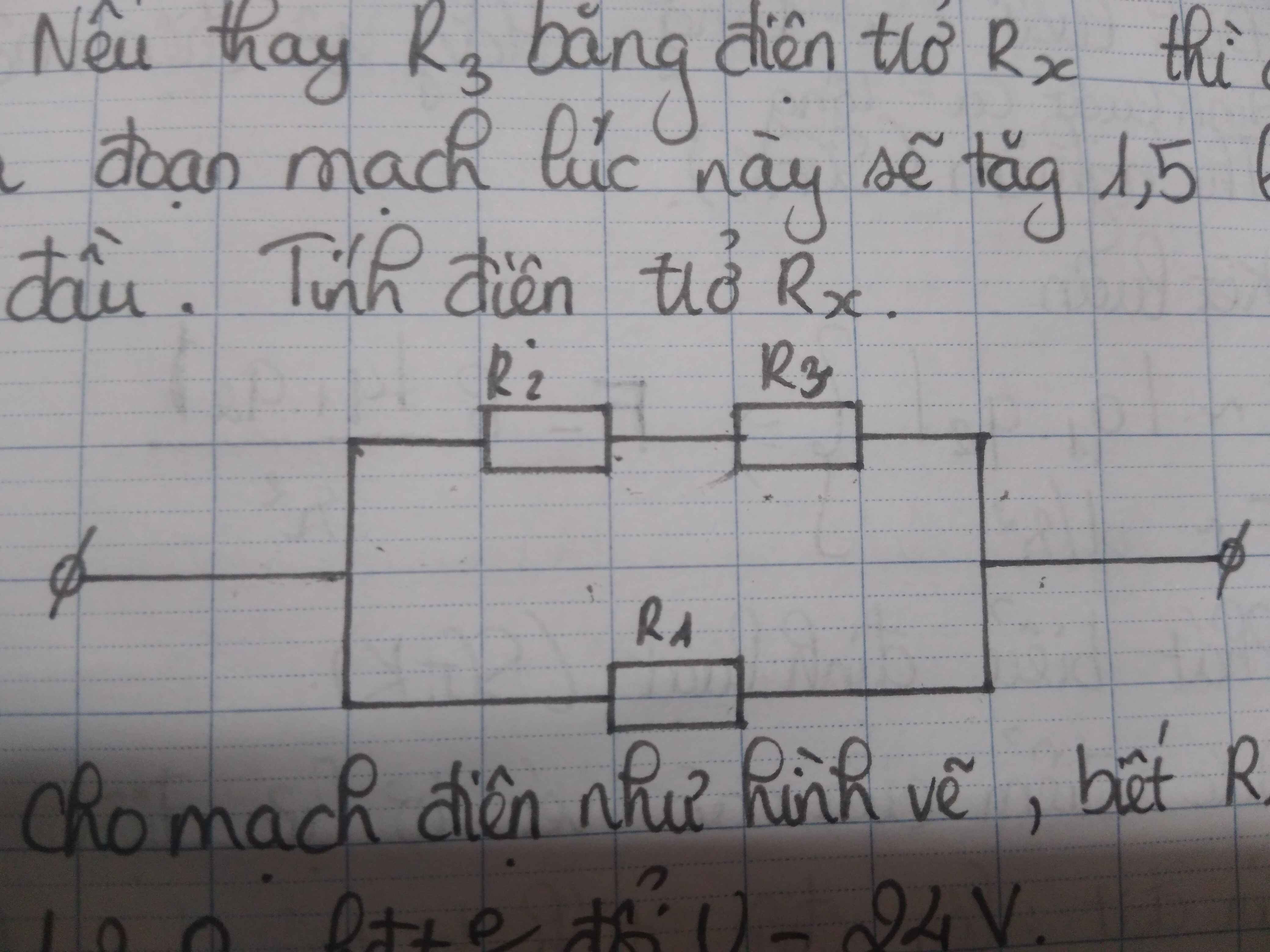
Sơ đồ mạch điện đâu bạn?
sơ đò mik ko có