Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

R1 nt R2
a,\(=>Rtd=R1+R2=39\left(om\right)\)
b,\(=>Um=Im.Rtd=39.2,5=97,5V\)
c, R1 nt R2 nt R3
\(=>I1=I2=I3=Im=2A\)
\(=>39+R3=\dfrac{U}{Im}=\dfrac{97,5}{2}=>R3=9,75\left(om\right)\)

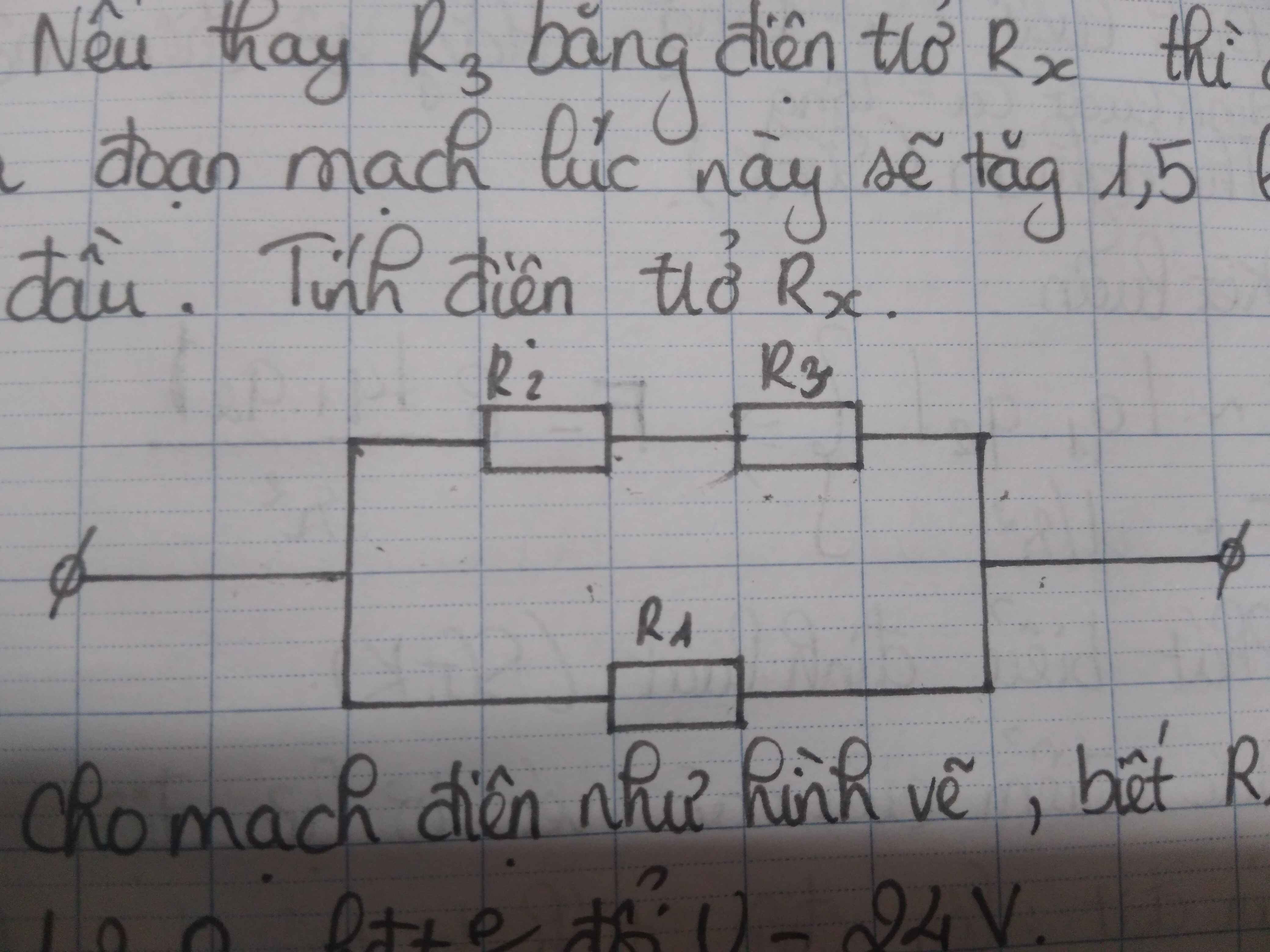
\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)

a,
b, CĐDĐ của mạch là:
Ta có: \(I=\dfrac{U}{R_{tđ}}=\dfrac{U}{R_1+R_2+R_3}=\dfrac{6}{3+5+7}=0,4\left(A\right)\)
c, Vì các điện trở R1, R2, R3 đc mắc nt
\(\Rightarrow I=I_1=I_2=I_3=0,4A\)
Mà R1 < R2 < R3
⇒ U1 < U2 < U3 (do HĐT tỉ lệ thuận với điện trở)
⇒ U3 lớn nhất
HĐT của R3:
Ta có: \(I=\dfrac{U_3}{R_3}\Leftrightarrow U_3=I.R_3=0,4.7=2,8\left(V\right)\)

Tóm tắt :
R1 = 6Ω
R2 = 9Ω
a) Rtđ = ?
b) I1 , I2 = ?
c) I = ?
a) Điện trở tương đương của đoạn mạch
\(R_{tđ}=R_1+R_2=6+9=15\left(\Omega\right)\)
b) Có : \(U_{AB}=U_1=U_2=12\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua điện trở R1
\(I_1=\dfrac{U_1}{R_1}=\dfrac{12}{6}=2\left(A\right)\)
Cường độ dòng điện chạy qua điện trở R2
\(I_2=\dfrac{U_2}{R_2}=\dfrac{12}{9}=1,3\left(A\right)\)
c) Cường độ dòng điện chạy trong mạch chính
\(I=I_1+I_2=2+1,3=3,3\left(A\right)\)
Chúc bạn học tốt
Mình xin lỗi bạn nhé , bạn sửa lại câu a) giúp mình :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{6.9}{6+9}=3,6\left(\Omega\right)\)

a, \(R1ntR2=>Rtd=R1+R2=50\left(om\right)\)
b,\(=>I1=I2=Im=\dfrac{U}{Rtd}=\dfrac{12}{50}=0,24A\)
c,\(=>I1=I3=Im=0,15A\)
\(=>R1+R3=\dfrac{U}{Im}=\dfrac{12}{0,15}=80\left(om\right)\)
\(=>R3=80-R1=60\left(om\right)\)

\(=>R1ntR2ntR3\)
\(=>Im=I3=I2=I1=2A\)
\(=>Rtd=\dfrac{U}{Im}=\dfrac{90}{2}=45\left(om\right)\)
\(=>Rtd=R1+R2+R3=R1+R1+\dfrac{R1}{4}=45\left(om\right)\)
\(=>R1=20\left(om\right)=R2\)
\(=>R3=\dfrac{R1}{4}=\dfrac{20}{4}=5\left(om\right)\)

\(R1ntR2ntR3\)
\(a,\Rightarrow R3=Rtd-R1-R2=20\Omega\)
\(b,\Rightarrow I1=I2=I3=1,2A\)
\(c,\Rightarrow Um=ImRtd=100.1,2=120V\)
\(\Rightarrow\left\{{}\begin{matrix}U1=I1.R1=54V\\U2=I2R2=42V\\U3=I3R3=24V\end{matrix}\right.\)