Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 thẻ trong số 6 thẻ.
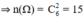
a. Gọi A: “ Hai điểm là đầu mút của cạnh của lục giác”
⇒ n(A) = 6 (Lục giác có 6 cạnh)
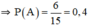
b. Gọi B: “ Hai điểm là đầu mút của đường chéo”
⇒ B = A− (Vì một đoạn thẳng chỉ có thể là một cạnh hoặc một đường chéo)
⇒ P(B) = 1 – P(A) = 1 – 0,4 = 0,6
c. Gọi C: “ Hai điểm là đầu mút của đường chéo nối hai đỉnh đối diện”
⇒ n(C) = 3
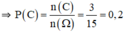

Giải:
Vì lấy 2 điểm nên:
\(C^2_6=15\rightarrow n\left(\Omega\right)=15\)
Gọi:
\(A\) là biến cố "2 thẻ lấy ra là 2 cạnh của lục giác"
\(B\) là biến cố "2 thẻ lấy ra là đường chéo của lục giác"
\(C\) là biến cố "2 thẻ lấy ra là đường chéo của 2 cạnh đối diện của lục giác"
a) \(n\left(A\right)=6\Rightarrow P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{6}{15}=\dfrac{2}{5}\)
b) \(B=\overline{A}\Rightarrow P\left(B\right)=1-P\left(A\right)=1-\dfrac{2}{5}=\dfrac{3}{5}\)
c) \(n\left(C\right)=6\Rightarrow P\left(C\right)=\dfrac{n\left(C\right)}{n\left(\Omega\right)}=\dfrac{3}{15}=\dfrac{1}{5}\)

Số vecto tạo từ 2n điểm là: \(A_{2n}^2\)
Đa giác đều 2n đỉnh có n đường chéo, cứ 2 đường chéo cho ta 1 hình chữ nhật tương ứng, do đó số hình chữ nhật có đỉnh là đỉnh của đa giác đều là: \(C_n^2\)
\(\Rightarrow A_{2n}^2=9C_n^2\Leftrightarrow\dfrac{\left(2n\right)!}{\left(2n-2\right)!}=\dfrac{9.n!}{2!.\left(n-2\right)!}\)
\(\Leftrightarrow2n\left(2n-1\right)=\dfrac{9n\left(n-1\right)}{2}\)
\(\Leftrightarrow n=5\)
dạ em chưa hiểu tại sao số vecto tạo từ 2n điểm và số hình chữ nhật có đỉnh là đỉnh của đa giác đều lại ra được như kia vậy ạ :(((

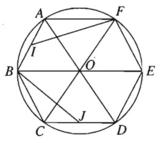
a) Phép quay tâm O góc 120 ο biến F, A, B lần lượt thành B, C, D; biến trung điểm I của AB thành trung điểm J của CD. Nên nó biến tam giác AIF thành tam giác CJB.
b) Phép quay tâm E góc 60 ο biến A, O, F lần lượt thành C, D, O.

Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt.
Từ 4 điểm ban đầu ta có 4 cách chọn điểm đầu và 3 cách chọn điểm cuối.
Do đó; có tất cả 4.3= 12 vecto được tạo ra.
Chọn D

Các vecto cùng phương O C → với có điểm đầu và điểm cuối là các đỉnh của lục giác
Chọn C.