Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài không đúng
ABCD.A'B'C'D' là lăng trụ thì AB=A'B' mà \(AB=a\) thì A'B' không thể bằng \(a\sqrt{2}\)

Đáp án C
Đường cao của hình lăng trụ là
h = V S A B C D = 3 a 3 a 2 = 3 a

Đáp án A
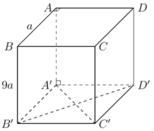
Ta có ABCD.A'B'C'D' là lăng trụ tứ giác đều nên có đáy là hình vuông và cạnh bên vuông góc với đáy.
Suy ra VABCD.A'B'C'D' = SABCD. AA' = a2. 9a = 9a3.

a) Với hình lăng trụ đứng ABC.ABC, diện tích tứ giác ABBA bằng 2a^2 và đáy ABC là tam giác vuông cân tại A, ABa. Thể tích khối lăng trụ ABC.ABC có thể tính bằng công thức: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Vì đáy ABC là tam giác vuông cân nên diện tích đáy là \(\frac{1}{2} \times a \times a = \frac{1}{2}a^2\). Chiều cao của lăng trụ chính là cạnh AB, vì tam giác ABa là tam giác vuông cân nên \(AB = \sqrt{2}a\). Do đó, thể tích khối lăng trụ ABC.ABC là: \(V = \frac{1}{3} \times \frac{1}{2}a^2 \times \sqrt{2}a = \frac{\sqrt{2}}{6}a^3\). b) Với hình lăng trụ đứng ABC.ABC, góc giữa (ABC) và (ABC) bằng 60°, ta cũng áp dụng công thức tính thể tích khối lăng trụ: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Diện tích đáy và chiều cao đã được tính tương tự như phần a), ta có thể tính được thể tích khối lăng trụ ABC.ABC.

Đáp án A.
Từ A dựng A H ⊥ A ' B ( H ∈ A ' B )
⇒ A H = a 3
1 A H 2 = 1 A A ' 2 + 1 A B 2
⇒ 1 A A ' 2 = 1 3 a 2 - 1 4 a 2 = 1 12 a 2
⇒ A A ' = 2 a 3 ⇒ V = 8 a 3 3

Đáp án C
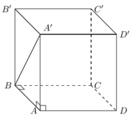
Diện tích đáy lăng trụ là a2.
Chiều cao của lăng trụ là A A ' = A ' B 2 - B A 2 = 4 a 2 - a 2 = a 3
Vậy thể tích lăng trụ là V = √3a3

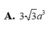
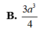

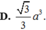

Lời giải:
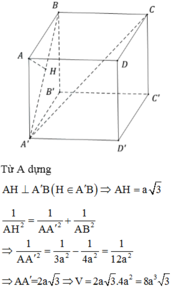
$ABCD.A'B'C'D'$ là lăng trụ đứng
Chiều cao: $AA'=\sqrt{AB'^2-A'B'^2}=\sqrt{(a\sqrt{2})^2-a^2}=a$
Thể tích lăng trụ:
$V=S_{ABCD}.AA'=a^2.a=a^3$ (đơn vị thể tích)