
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

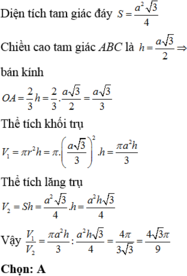

Đáp án A

Diện tích của tam giác đều cạnh a là a 2 3 4 . Lăng trụ tm giác đều các cạnh bên vuông góc với đáy nên thể tích của lăng trụ đã cho V = a . a 2 3 4 = a 3 3 4

Đáp án B
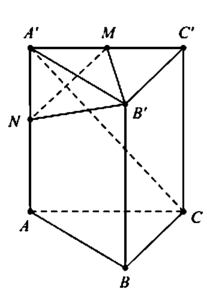 Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Suy ra M ∈ m p P . Kẻ M N ⊥ A ' C ( N ∈ A A ' ) ⇒ N ∈ m p P
Thiết diện cắt bởi mặt phẳng (P) và lăng trụ là tan giác B’MN
Hai tam giac A’C’C và NA’M đồng dạng ⇒ A ' N = 1 2 A ' M = a 4
Thể tích tứ diện A'B'MN là V 1 = 1 3 A ' N . S ∆ A ' B ' M = a 3 3 96
Thể tích lăng trụ là V = A A ' . S ∆ A B C = a 3 3 2 . Vậy V 1 V 2 = 1 47 .

Đáp án C
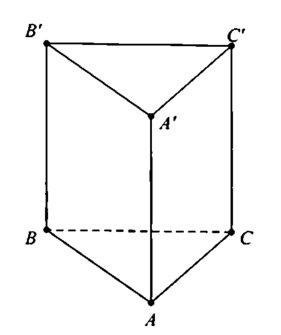 Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC
Ta có: R = B C 2 sin A = a 2 sin 60 ° = a 3
Thể tích V của khối trụ ngoại tiếp lăng trụ là:
V = πR 2 h = π a 3 2 . h = πa 2 h 3 .

Đáp án B
Xét khối lăng trụ tam giác đều ABC.A’B’C’ ⇒ A A ' = h
Đặt A B = x suy ra bán kính đường tròn ngoại tiếp Δ A B C là R = x 3 3
Khi đó a = x 3 3 ⇒ x = a 3
Thể tích cần tìm là:
V = h S = h a 3 2 3 4 = 3 3 a 2 h 4