Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Kẻ $SH$ vuông góc với $SB$
Vì $SA$ vuông góc với đáy nên \(SA\perp BC\). Tam giác $ABC$ vuông tại $B$ nên \(AB\perp BC\)
Ta có:
\(\left\{\begin{matrix}
SA\perp BC\\
AB\perp BC\end{matrix}\right.\Rightarrow (SAB)\perp BC\)
Mà \(AH\subset (SAB)\Rightarrow AH\perp BC\)
Kết hợp với \(AH\perp SB\Rightarrow AH\perp (SBC)\)
Do đó \(d(A,(SBC))=AH\)
Xét tam giác $SAB$ vuông tại $A$ có đường cao $AH$ thì theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{SA^2}=\frac{1}{a^2}+\frac{1}{a^2}\)
\(\Rightarrow AH=\frac{a\sqrt{2}}{2}\)
Vậy \(d(A,(SBC))=\frac{a\sqrt{2}}{2}\)

Đáp án là B
Ta có đáy là hı̀nh thoi có một góc
120
0
nên diện tı́ch đáy bằng 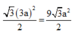
do lăng trụ đứng nên ta có thể tı́ch khối lăng trụ bằng 27 3 a 3 2
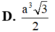
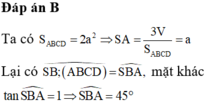
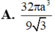
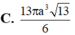
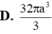
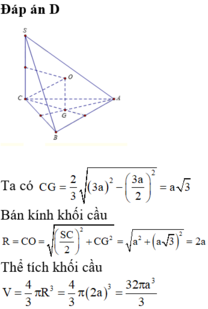
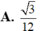
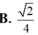
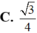
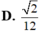
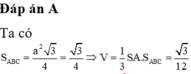
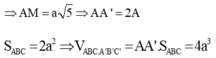
Đáp án D