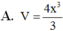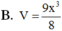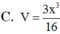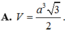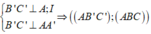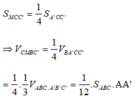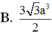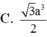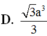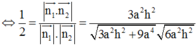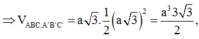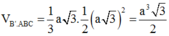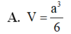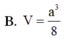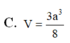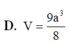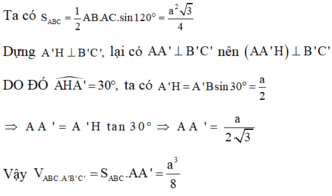Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

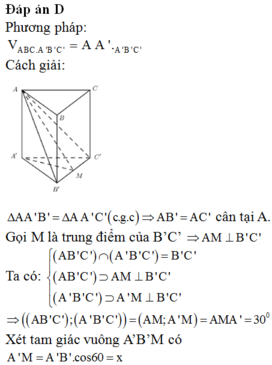
Chọn D
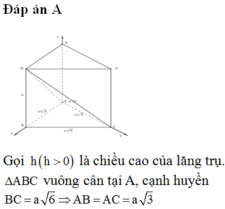
Vì tam giác ABC vuông cân tại A, cạnh BC = a√6 nên AB = AC = a√3.
Chọn hệ trục tọa độ Oxyz sao cho A (0;0;0), B (0; a√3; 0), C (a√3;0;0), A' (0;0;z) (z > 0).
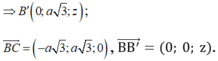
VTPT của (BCC'B') là:
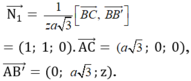
VTPT của mặt phẳng (BA'C) là:
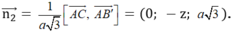
Vì góc giữa mặt phẳng và mặt phẳng bằng nên:
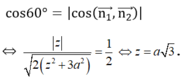
Vậy thể tích của khối lăng trụ ABC.A'B'C' là:
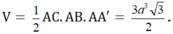

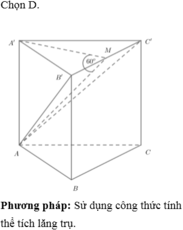
Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
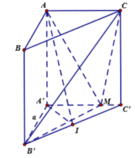
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)