Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
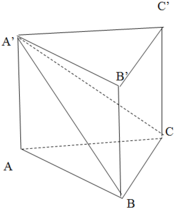
Ta có A’C = a 13 , A’B = 3a, BC = 2a
Suy ra tam giác A’BC vuông tại B
Ta có ![]()

Đáp án A
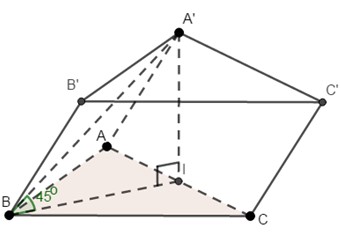
Khoảng cách giữa hai mặt đáy là h = AH = A’H.tan A A ' H ^ = a 3 2 . tan 30 0 = a 2

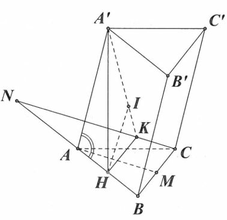
Đáp án D
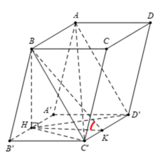
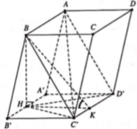
Gọi H là trung điểm của BC, kẻ H K ⊥ C ' D ' K ∈ C ' D '
Suy ra B H ⊥ A ' B ' C ' D ' ⇒ A C ' D ' ; A ' B ' C ' D ' ^ = B K H ^
Tam giác A’C’D’ đều cạnh 2 a ⇒ H K = d A ' ; C ' D ' = a 3
Tam giác BHK vuông tại H ⇒ B H = tan 60 ∘ x H K = 3 a
Diện tích hình thoi A’B’C’D’ là S A ' B ' C ' D ' = 2 a 2 3 .
Vậy thể tích khối lăng trụ ABC.A’B’C’D’ là V = B H . S A ' B ' C ' D ' = 3 a .2 a 2 3 = 6 3 a 3

Đáp án D
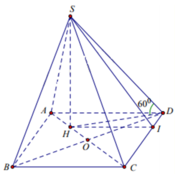
Gọi I ∈ C D sao cho H I / / A D .
Ta có H I A D = C H C A ⇔ H I = A D . C H C A = 2 a . 3 4 = 3 a 2 .
Và H D = D O 2 + H O 2 = D O 2 + D O 2 4 = D O 5 2 .
Mà 2 D O 2 = 4 a 2 ⇒ D O = a 2
⇒ H D = a 2 . 5 2 = a 10 2 ⇒ S H = H D . tan 60 ∘ = a 30 2 .
Vậy α = S I H ^ ⇒ tan α = S H H I = a 30 2 3 a 2 = 30 2 .
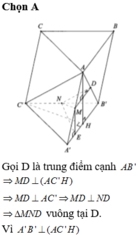
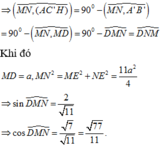

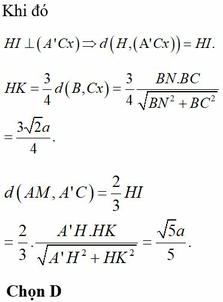

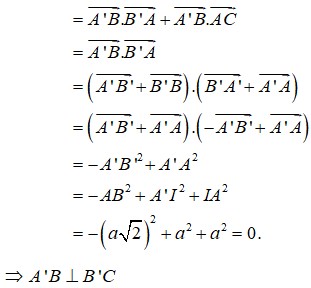


Đáp án D
Phương pháp: Cho hai mặt phẳng (α) và (β) cắt nhau, ta xác định góc giữa (α) và (β) như sau:
- Tìm giao tuyến ∆ của hai mặt phẳng (α) và (β).
- Tìm trong mỗi mặt phẳng (α), (β) một đường thẳng 𝑎, cùng cùng vuông góc với ∆ và cùng cắt ∆ tại điểm .
- Xác định góc giữa 𝑎 và 𝑏.
Cách giải: Gọi H là trung điểm của A’B’ => AH ⊥ (A’B’C’)
Kẻ HJ, A'K' ⊥ B'C', (J, K' ∈ B'C'), AK ⊥ BC, (K ∈ BC)
HJ//A'K', A'K'//AK => HJ//AK => H,J,A,K đồng phẳng
Vì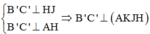
Ta có: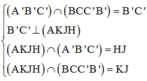
=> ((BCC'B');(A'B'C')) = (KJ;HJ)
A ' B ' K ' ^ = 180 0 - 120 0 = 60 0
=> A'K' = A'B' . sin 60 0
Xét ∆B’HC’ : H'C =
∆AHC’ vuông tại H => AH = HC.tanC’ = HC.tan(AC’;(A’B’C’)) (vì AH ⊥ (A’B’C’))
Xét hình thang vuông AKJH:
Kẻ
Vì AK//HJ