Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
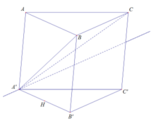
Xét (A’B’C’) và (A’BC) có:
A’ là điểm chung
B’C’ // BC
giao tuyến của 2 mặt phẳng là đường thẳng d qua A’ song song với B’C’
⇒ d và B’C’ đồng phẳng
Mà d chứa A’
⇒ d thuộc mặt phẳng (A’B’C’)
Mà H ∈ A’B’ ⇒ H ∈ (A’B’C’)
⇒ Mặt phẳng đi qua d và H, cắt tứ diện ABC. A’B’C’ là (A’B’C’)
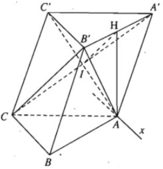
a) Ta có tứ giác AA’CC’ là hình bình hành suy ra A’C cắt AC’ tại trung điểm I của mỗi đường.
Do đó IH // CB′ ( đường trung bình của tam giác CB’A’)
Mặt khác IH ⊂ (AHC′) nên CB′ // (AHC′)
b) Ta có:
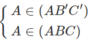
suy ra, ⇒ A là điểm chung của (AB’C’) và (ABC)
Mà
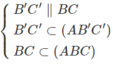
Nên (AB′C′) ∩ (ABC) = Ax
Và Ax // BC // B′C′
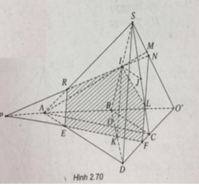
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
c) Đường thẳng qua I song song với SD cắt BD tại K.
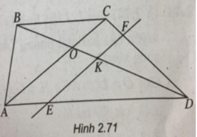
Do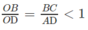 
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.
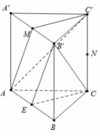
(a)đi pua cc" và song song với 2 đt AH,CB'