Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B'N=2BN\Rightarrow BN=\dfrac{1}{3}BB'=2a\)
Qua N lần lượt kẻ các đường thẳng song song AB và BC, chúng cắt AA' tại E và CC' tại F
\(\Rightarrow AE=BN=CF=2a\Rightarrow PF=ME=\dfrac{6a}{2}-2a=a\)
\(NF=NE=AB=BC=a\)
\(\Rightarrow MN=NP=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow S_{MNP}=\dfrac{a^2\sqrt{7}}{4}\) (công thức Herong, hoặc kẻ NH vuông góc MP và tính NH theo Pitago với tam giác MNP cân tại N)
\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
Do MA, NB, PC vuông góc (ABC) \(\Rightarrow\) ABC là hình chiếu vuông góc của MNP lên (ABC)
\(\Rightarrow cos\alpha=\dfrac{S_{ABC}}{S_{MNP}}=\sqrt{\dfrac{3}{7}}\Rightarrow\alpha\)

Đáy ABC vuông cân tại B thì ACB=BAC=45\(^0\)chứ bạn.
Bạn có gõ nhầm đề không?
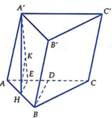
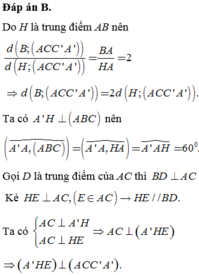
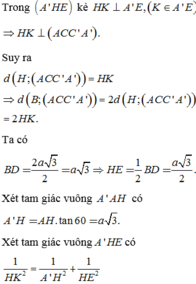
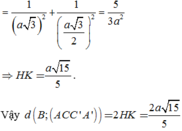
\(\widehat{A'AH}=60^0\Rightarrow A'H=AH.tan60^0=\frac{a\sqrt{2}}{2}\sqrt{3}=\frac{a\sqrt{6}}{2}\)
Do \(CB=2HB\Rightarrow d\left(C;\left(ABB'A'\right)\right)=2d\left(H;\left(ABB'A'\right)\right)\)
Từ H kẻ \(HM\perp AB\Rightarrow HM=\frac{1}{2}AC=\frac{a}{2}\)
Từ H kẻ \(HN\perp A'M\Rightarrow HN\perp\left(ABB'A'\right)\Rightarrow HN=d\left(H;\left(ABB'A'\right)\right)\)
\(\frac{1}{HN^2}=\frac{1}{A'H^2}+\frac{1}{HM^2}\Rightarrow HN=\frac{A'H.HM}{\sqrt{A'H^2+HM^2}}=\frac{a\sqrt{42}}{14}\)
\(\Rightarrow d\left(C;\left(ABB'A'\right)\right)=\frac{a\sqrt{42}}{7}\)