Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(\bullet\)Nếu \(x\geq \frac{1}{2}\Rightarrow K=x-\frac{1}{2}+\frac{3}{4}-x=\frac{1}{4}\)
\(\bullet\) Nếu \(x<\frac{1}{2}\Rightarrow K=\frac{1}{2}-x+\frac{3}{4}-x=\frac{5}{4}-2x\)
Vì \(x<\frac{1}{2}\Rightarrow \frac{5}{4}-2x>\frac{5}{4}-1=\frac{1}{4}\)
Do đó \(K_{\min}=\frac{1}{4}\)
Hàm hiển nhiên không có max. Xét hàm \(\frac{5}{4}-2x\), với giá trị của \(x<\frac{1}{2}\), càng nhỏ thì $K$ càng lớn đến dương vô cùng.
TH1:Nếu x-\(\dfrac{1}{2}=0\Rightarrow x=\dfrac{1}{2}\)
\(\Rightarrow\)K=\(\left|\dfrac{1}{2}-\dfrac{1}{2}\right|+\dfrac{3}{4}-\dfrac{1}{2}=\dfrac{1}{4}\)
TH2:Nếu x-\(\dfrac{1}{2}>0\Rightarrow x>\dfrac{1}{2}\Rightarrow\left|x-\dfrac{1}{2}\right|=x-\dfrac{1}{2}\)
\(\Rightarrow K=x-\dfrac{1}{2}+\dfrac{3}{4}-x=\dfrac{1}{4}\)
TH3:Nếu \(x-\dfrac{1}{2}< 0\Rightarrow x< \dfrac{1}{2}\Rightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}-x\)
\(\Rightarrow K=\dfrac{1}{2}-x+\dfrac{3}{4}-x\)
\(\Rightarrow K=\dfrac{5}{4}-2x< \dfrac{1}{4}\)
Vậy Max K=\(\dfrac{1}{4}\Leftrightarrow x\ge\dfrac{1}{2}\)

|x-1/2| =x-1/2 khi x >= 1/2
=> Min K =1/4 khi x>=1/2
không có max

a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
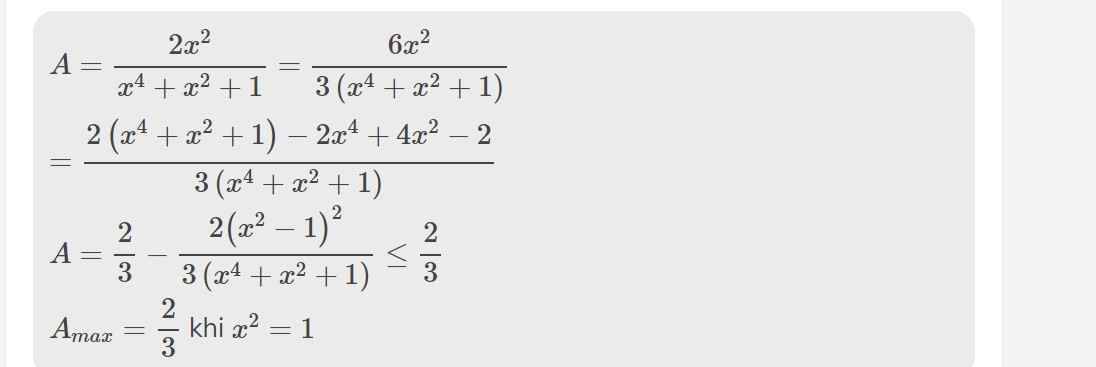

\(b,Q=-5x^2-4x+1\)
\(=-5\left(x^2+\dfrac{4}{5}x+\dfrac{4}{25}\right)+\dfrac{9}{5}\)
\(=-5\left(x+\dfrac{2}{5}\right)^2+\dfrac{9}{5}\)
Với mọi giá trị của x ta có:
\(-5\left(x+\dfrac{2}{5}\right)^2\le0\)
\(\Rightarrow-5\left(x+\dfrac{2}{5}\right)^2+\dfrac{9}{5}\le\dfrac{9}{5}\)
Vậy MaxQ = \(\dfrac{9}{5}\)
Để Q = \(\dfrac{9}{5}\) thì \(x+\dfrac{2}{5}=0\Rightarrow x=-\dfrac{2}{5}\)
\(c,K=x\left(x-3\right)\left(x-4\right)\left(x-7\right)\)
\(=x\left(x-7\right)\left(x-3\right)\left(x-4\right)\)
\(=\left(x^2-7x\right)\left(x^2-7x+12\right)\)
Đặt \(x^2-7x+6=t\) , ta có:
\(K=\left(t-6\right)\left(t+6\right)\)
\(=t^2-36\)
\(=\left(x^2-7x+6\right)^2-36\)
Với mọi giá trị của x ta có:
\(\left(x^2-7x+6\right)^2\ge0\Rightarrow\left(x^2-7x+6\right)^2-36\ge-36\)
Vậy Min K = -36
Để K = - 36 thì \(x^2-7x+6=0\)
\(\Leftrightarrow x^2-x-6x+6=0\)
\(\Leftrightarrow x\left(x-1\right)-6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=6\\x=1\end{matrix}\right.\)
a)\(P=2x^2-8x+1\)
=\(2\left(x^2-4x+4\right)-7\)
=\(2\left(x-2\right)^2-7\)
Với mọi x thì \(2\left(x-2\right)^2>=0\)
=>\(2\left(x-2\right)^2-7>=-7\)
Hay \(P>=-7\) với mọi x
Để \(P=-7\) thì
\(\left(x-2\right)^2=0\)
=>\(x-2=0\)
=>\(x=2\)
Vậy...
Các câu sau tương tự

dtydudjgbjbjbjvjkkdxkdiuryyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyykkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhrrrrrrrrrrrrrrrrrrrrrrrrrrnmdchytfegttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttdyyyyyyyyyyyyyyyyyyyyyyyyrrrrrrrrrrrrrrrrrrrrrrrrr
ASDFGHJKL;''\\\\\\\\\\\\\\09876212EFGNM,///////////////,HHVSZZCCCCCCCCCCCCCCBBBBBBBBBBBBBBMMMMMMMMMMMMJJXGGJBDU.LH7UJKI,M MYN YBRROP
IJUL[
-PIIGDAAQWRTYUIOLP;LNBF1954DGW22568997TVV32V456

Ta có : \(P=2x^2-8x+1=2\left(x^2-4x\right)+1=2\left(x^2-4x+4-4\right)+1=2\left(x-2\right)^2-7\)
Vì \(2\left(x-2\right)^2\ge0\forall x\)
Nên : \(P=2\left(x-2\right)^2-7\ge-7\forall x\in R\)
Vậy \(P_{min}=-7\) khi x = 2