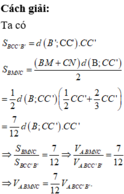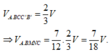
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Ta có:
V A B C . A ' B ' C ' = d ( A ; ( A ' B ' C ' ) ) . S ∆ A ' B ' C ' = V
V A . A ' B ' C ' = 1 3 . d ( A ; ( A ' B ' C ' ) ) . S ∆ A ' B ' C ' = V 3

Đáp án A
Ta có V A B C . A ' B ' C ' = V M . A B C + V M . A ' B ' C ' + V M . B C C ' B ' = 1 3 V A B C . A ' B ' C ' + V M . B C C ' B ' ⇒ V M . B C C ' B ' = 2 V 3

Chọn B.
Phương pháp:
Áp dụng công thức tính thể tích lăng trụ: V = B.h trong đó: V là thể tích lăng trụ, B là diện tích đáy của lăng trụ, h là chiều cao của lăng trụ.
Cách giải:
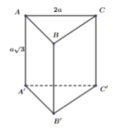
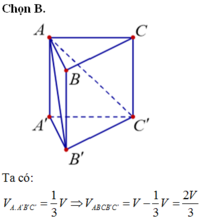
Diện tích tam giác đều ABC có cạnh 2a là:
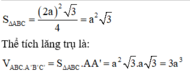

Đáp án là D.
V A B C . A ' B ' C ' = a . a 2 3 4 = a 3 3 4 .

Chọn B.
Phương pháp:

+) So sánh diện tích hình thang BMNC và diện tích hình bình hành BCC’B’ từ đó suy ra tỉ số thể tích V A . B M N C V A . B C C ' B '
+) So sánh V A . B C C ' B ' với V.