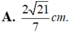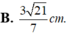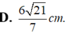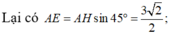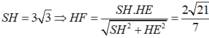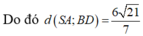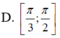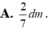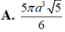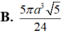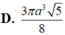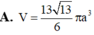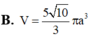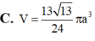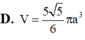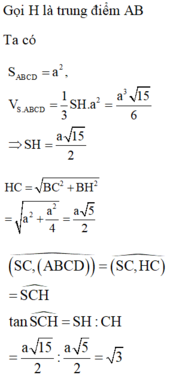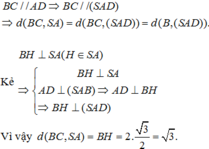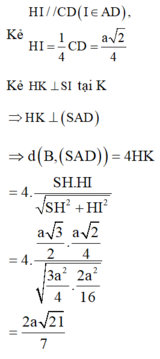Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
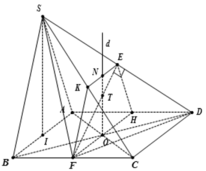
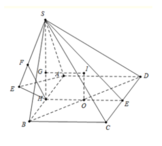
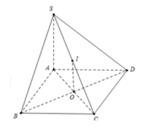
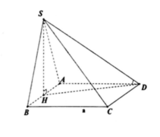
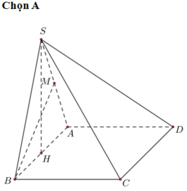
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
![]()
Bán kính mặt cầu là
![]()
+ Xét tam giác vuông TOB vuông tại B, ta có
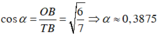

Hướng dẫn: D
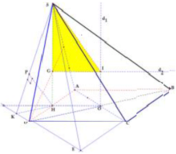
+ Gọi x > 0 là cạnh của hình vuông ABCD và H là trung điểm cạnh AD
+ Dễ dàng chứng minh
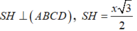
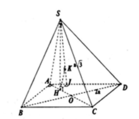
+ Gọi O = AC ∩ BD và G là trọng tâm ∆ A S D , đồng thời d 1 , d 2 lần lượt là 2 trục đường tròn ngoại tiếp ABCD, ∆ S A D ( d 1 qua O và // SH, d 2 qua G và //AB)
⇒ I = d 1 ∩ d 2 là tâm mặt cầu ngoại tiếp khối chóp S. ABCD ⇒ R = SI
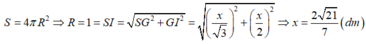
(trong video bài giảng chữa đề, phần này Thầy dùng công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp trong trường hợp chóp có mặt bên vuông góc với mặt đáy).
+ Gọi E là điểm thỏa ADEC là hình bình thành
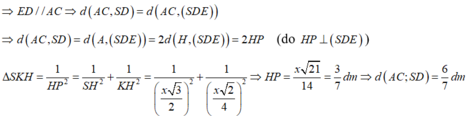

Đáp án A.
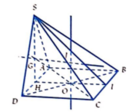
Trong mặt phẳng (ABCD) gọi: ![]() H là trung điểm AD.
H là trung điểm AD.
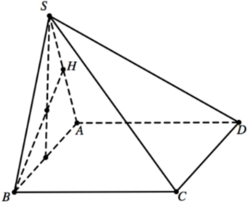
Gọi I,J lần lượt là trung điểm của BC và G là trọng tâm ∆ SAD
Đường thẳng d qua O và vuông góc với (ABCD) gọi là trục của đường tròn ngoại tiếp đáy (ABCd).
∆ qua G và vuông góc với (SAD) là trục của đường tròn ngoại tiếp (SAD).
Trong mặt phẳng (SHI), gọi I = ∆ ∩ d
=> J cách đều các đỉnh của hình chóp
=> J là tâm mặt cầu ngoại tiếp S.ABCD có bán kính
R = JD = ![]()
Có ![]()