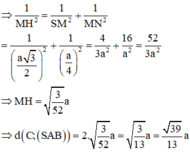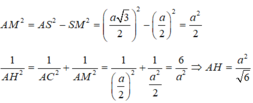Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
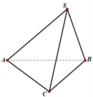
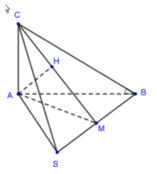
Gọi M là trung điểm của BC
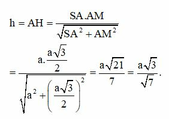
Kẻ A H ⊥ S M ⇒ d A ; S B C = A H
S A = a , A M = a 3 2 1 A H 2 = 1 S A 2 + 1 A M 2 = 1 a 2 + 1 3 a 2 ⇒ A H = A 3 7

Đáp án B.
Gọi H là trung điểm của BC khi đó S H ⊥ B C do S B C ⊥ A B C ⇒ S H ⊥ A B C
Lại có: C B = 2 C H ⇒ d C ; S A B = 2 d H ; S A B
Dựng H E ⊥ A B H F ⊥ S E ⇒ d H = H F
Mặt khác H E = A C 2 = 1 2 B C . sin A B C ^ = a 4 ; S H = a 3 2
Do đó H F = S H . H E S H 2 + H E 2 = a 39 26 ⇒ d c = a 39 13

Chọn C.
Phương pháp:
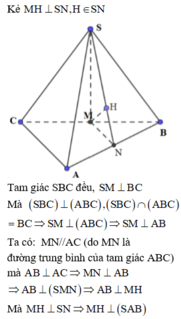
Đưa về dựng khoảng cách từ M đến (SAB) với M là trung điểm của BC.
Cách giải:
Gọi M, N lần lượt là trung điểm của BC, AB.