Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải:
Để i n là số nguyên dương thì n là số nguyên dương chia hết cho 4
Lời giải:
Xét n=2k khi đó ![]() là số nguyên dương khi k chẵn.
là số nguyên dương khi k chẵn.
Kết hợp với ![]() suy ra
suy ra 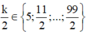 và
và ![]() là số chẵn.
là số chẵn.
Với mỗi bộ số 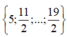 có 2 số k thỏa mãn,
có 2 số k thỏa mãn, 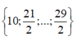 có 3 số k thỏa mãn.
có 3 số k thỏa mãn.
Vậy có tất cả 2.5+3.4=22 số thỏa mãn yêu cầu bài toán.

Đáp án B
Phương pháp.
Gọi ![]() . Sử dụng giả thiết để tìm a, bsuy ra giá trị của z. Sử dụng kết quả này để tìm giá trị của m và kết luận.
. Sử dụng giả thiết để tìm a, bsuy ra giá trị của z. Sử dụng kết quả này để tìm giá trị của m và kết luận.
Lời giải chi tiết.
Giả sử ![]() Khi đó ta có
Khi đó ta có
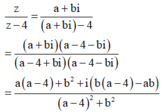
Để ![]() là số thuần ảo thì ta phải có
là số thuần ảo thì ta phải có
![]()
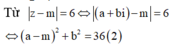
Từ (1) suy ra ![]() thay vào (2) ta nhận được
thay vào (2) ta nhận được
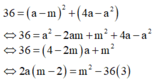
Nếu m=2 thì (3) vô nghiệm
Nếu m
≠
2 thì từ (3) suy ra ![]()
Vì ![]() nên để có duy nhất một số phức z thỏa mãn điều kiện đã cho thì b=0
nên để có duy nhất một số phức z thỏa mãn điều kiện đã cho thì b=0
Ta nhận được a=0 hoặc a=4
với a=4 thì z=a+bi=4. Loại vì ![]() là số thuần ảo
là số thuần ảo
vậy a=b=0
⇒
z=0. Khi đó ![]()
Tổng các phần tử của S là 6+(-6)=0

Đáp án B

Phương trình (1) có hai nghiệm dương phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt lớn hơn 1.
Bảng biến thiên của hàm số y = t 2 - 10 t
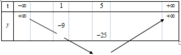
Phương trình (2) có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi -25< m < -9
Vậy S = {-24;-23;...;-10} và n(S) =15


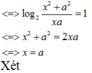
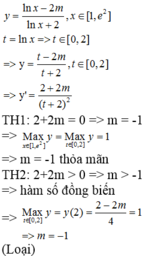
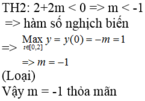
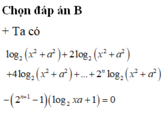




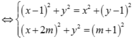
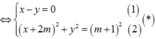

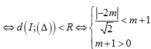

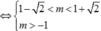


Đáp án A