Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

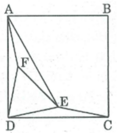
Xét ∆ EDC và ∆ FDA, tacó: ∠ (EDC) = ∠ (FDA) = 15 0
DC = AD (gt)
∠ (ECD) = ∠ (FAD) = 15 0
Suy ra: ∆ EDC = ∆ FDA (g.c.g)
⇒ DE = DF
⇒ ∆ DEF cân tại D
Lại có: ∠ (ADC) = ∠ (FDA) + ∠ (FDE) + ∠ (EDC)
⇒ ∠ (FDE) = ∠ (ADC) -( ∠ (FDA) + ∠ (EDC) )= 90 0 - ( 15 0 + 15 0 ) = 60 0
Vậy ∆ DEF đều.

Do tam giác FCD đều nên FC = DC = CB. Do đó tam giác BCF cân tại C nên \(\widehat{FBC}=\dfrac{180^o-\widehat{FCB}}{2}=\dfrac{180^o-150^o}{2}=15^o=\widehat{EBC}\).
Vậy B, E, F thẳng hàng.
Trúc Giang Bạn cần giải thích đoạn nào vậy?
Tam giác BCF cân tại C nên \(\widehat{FBC}=\widehat{BFC}\).
Do đó \(\widehat{FBC}+\widehat{BFC}+\widehat{FCB}=180^o\Leftrightarrow\widehat{FCB}+2\widehat{FBC}=180^o\Leftrightarrow\widehat{FBC}=\dfrac{180^o-\widehat{FCB}}{2}\).
Do đó \(\widehat{FBC}=\widehat{EBC}\) mà E, F cùng thuộc 1 nửa mf bờ BC nên E, B, F thẳng hàng.

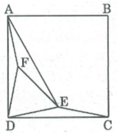
Xét ∆ ADE và ∆ BCE , ta có:
ED = EC (vì AEDC cân tại E)
∠ (ADE) = ∠ (BCE) = 75 0
AD = BC (gt)
Suy ra: ∆ ADE = ∆ BCE (c.g.c)
⇒ AE = BE (1)
* Trong ∆ ADE, ta có:
∠ (AFD) = 180 0 – ( ∠ (FAD) + ∠ (FDA) ) = 180 0 – ( 15 0 + 15 0 ) = 150 0
∠ (AFD) + ∠ (DFE) + ∠ (AFE) = 360 0
⇒ ∠ (AFE) = 360 0 - ( ∠ (AFD) + ∠ (DFE) ) = 360 0 – ( 150 0 + 60 0 ) = 150 0
* Xét ∆ AFD và ∆ AFE, ta có: AF cạnh chung
∠ (AFD) = ∠ (AFE) = 150 0
DE = EF (vì ∆ DFE đều)
Suy ra: ∆ AFD = ∆ AFE (c.g.c) ⇒ AE = AD
Mà AD = AB (gt)
Suy ra: AE = AB (2)
Từ (1) và (2) suy ra: AE = AB = BE
Vậy ∆ AEB đều.

Ta có : ADCˆ=ADEˆ+EDCˆADC^=ADE^+EDC^
=> 90O=ADEˆ+15O90O=ADE^+15O
=> ADEˆ=75OADE^=75O
Tương tự ta cũng có : BCEˆ=75oBCE^=75o
Xét ΔADEΔADE và ΔBCEΔBCE có :
AD = BC (do ABCD à hình vuông)
ADEˆ=BCEˆ(=75o)ADE^=BCE^(=75o)
DE=ECDE=EC (do tam giác ECD cân tại E- gt)
=> ΔADEΔADE = ΔBCEΔBCE (c.g.c)
=> AE = BE (2 cạnh tương ứng)
Mà : AD = AE
=> ΔADEΔADE cân tại A
Xét ΔADEΔADE ta có :
ADEˆ=AEDˆ=75oADE^=AED^=75o (tính chất tam giác cân)
=> DAEˆ=180O−(ADEˆ+AEDˆ)DAE^=180O−(ADE^+AED^)
=> DAEˆ=180O−2.75O=30ODAE^=180O−2.75O=30O
Chứng minh tương tự ta có : CBEˆ=30oCBE^=30o
Có : ABEˆ=ABCˆ−CBEˆ=90O−30O=60OABE^=ABC^−CBE^=90O−30O=60O
BAEˆ=BADˆ−EADˆ=90O−30O=60OBAE^=BAD^−EAD^=90O−30O=60O
Xét ΔABEΔABE có :
ABEˆ+BAEˆ+AEBˆ=180OABE^+BAE^+AEB^=180O
=> AEBˆ=180O−2.60O=60OAEB^=180O−2.60O=60O
Thấy : ABEˆ=BAEˆ=AEBˆ=60oABE^=BAE^=AEB^=60o
=> ΔABEΔABE là tam giác đều (đpcm)

ko biết