Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có DM song song và bằng BN nên BMDN là hình bình hành (vì có 2 cạnh đối song song và bằng nhau)
b) Tam giác CDN bằng tam giác DAP (cạnh - góc - cạnh)
=> Góc D1 = góc A1
Ta lại có Góc D2 + Góc D1 = Góc D = 90 độ
=> Góc D2 + Góc A1 = 90 đo
Trong tam giác KAD có tổng 2 góc A và D bằng 90 độ nên góc K bằng 90 độ
=> AP vuông góc với DN
c) Tương tự câu b ta có BM vuông góc với AP
=> BM // DN (vì cùng vuông góc vời AP)
=> BMKN là hình thang.
Theo câu b tam giác KAD vuông tại K có KM là trung tuyến ứng với cạnh huyền => KM = 1/2 AD
=> KM = BN
=> BMKN là hình thang cân
d) \(DP=\frac{1}{2}\sqrt{5},AP=\sqrt{5-\frac{1}{4}5}=\frac{\sqrt{15}}{2}\)
\(DP^2=PK.PA\)
=> \(PK=\frac{DP^2}{PA}=\frac{\frac{5}{4}}{\frac{\sqrt{15}}{2}}=\frac{\sqrt{15}}{6}\)
=> \(\frac{PK}{PA}=\frac{\frac{\sqrt{15}}{6}}{\frac{\sqrt{15}}{2}}=\frac{1}{3}\)
=> Đường cao hạ từ K xuống DC bằng 1/3 đường cao hạ từ A xuống DC
=> Đường cao hạ từ K xuống DC = \(\frac{1}{3}\sqrt{5}\)
=> Đường cao hạ từ K xuống MN bằng \(\frac{1}{2}\sqrt{5}-\frac{1}{3}\sqrt{5}=\frac{\sqrt{5}}{6}\)
=> Diện tích KMN bằng \(\frac{1}{2}.MN.KH_2=\frac{1}{2}\sqrt{5}\frac{\sqrt{5}}{6}=\frac{5}{12}\)

https://olm.vn/hoi-dap/detail/96788252350.html
Tham khảo ở link này (mình gửi cho)
Hoc tốt!!!!!!!!!!!!

Bạn tìm được 3 cạnh thì áp dụng công thức Hơ rong để tính .

mk cũng hk lớp 8 nhưng chưa hok tới bài hình chữ nhật sorry bn!! ![]()

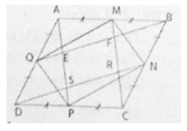
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2

a) Xét tam giác ACD có: AF=FC (gt) ; DK=KC (gt)
=> FK là đường trung bình của tam giác ACD
=> FK//AD
=> ADKF là hình thang
Chứng minh tương tự t cũng có: ME là đường trung bình của tam giác ABD
=> ME // AD mà FK//AD (cmt)
=> ME//FK (1)
Chứng minh tương tự ta cũng có:
MF là đường trung bình tam giác ABC , EK là đường trung bình tam giác DBC
=> MF//BC ; EK // BC
=> MF//EK (2)
Từ (1) và (2) ta có: EMFK là hình bình hành