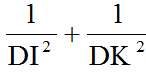Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

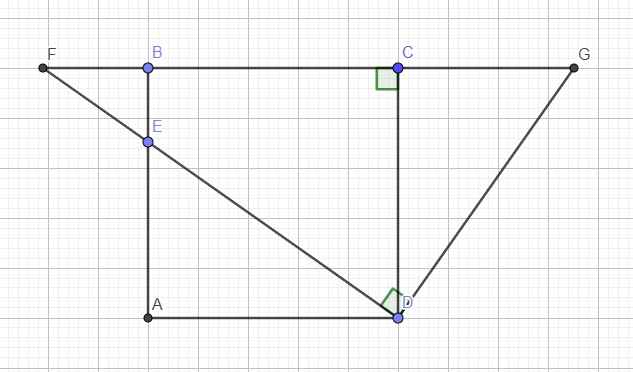
Xét hai tam giác vuông \(DAE\) và DCG:
\(\widehat{A}=\widehat{C}=90^0\)
\(AD=CD\) (cạnh hình vuông)
\(\widehat{ADE}=\widehat{CDG}\) (cùng phụ \(\widehat{CDE}\))
\(\Rightarrow\Delta DAE=\Delta DCG\left(g.c.g\right)\)
\(\Rightarrow DE=DG\)
\(\Rightarrow\Delta DEG\) cân tại D

Xét hai tam giác vuông ADI và CDL có:
AD = CD (cạnh hình vuông)
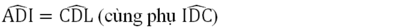
Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)
Suy ra DI = DL hay ΔDIL cân. (đpcm)

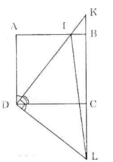
a) Xét hai tam giác vuông ADI và CDL có:
AD = CD (cạnh hình vuông)
![]()
Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)
Suy ra DI = DL hay ΔDIL cân. (đpcm)
b) Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:
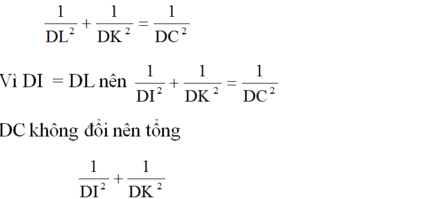
không đổi khi I thay đổi trên cạnh AB. (đpcm)

a) \(_{\Delta}\) ADI và \(\Delta\) DCL có:
góc DAI = góc DCL = \(90^0\) (gt)
AD=CD( gt)
góc ADI = góc CDL ( cùng phụ góc IDC)
=> \(\Delta\) ADI = \(\Delta\) CDL ( ch-gn) => DI =DL ( cạnh tương ứng)
=> Tam giác DIL cân
b) Tam giác DLK vuông tại D=> \(\dfrac{1}{C\text{D}^2}=\dfrac{1}{DK^2}+\dfrac{1}{DL^2}\)
=> \(\dfrac{1}{C\text{D}^2}=\dfrac{1}{DK^2}+\dfrac{1}{DI^2}\) ( DI = DL)