Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

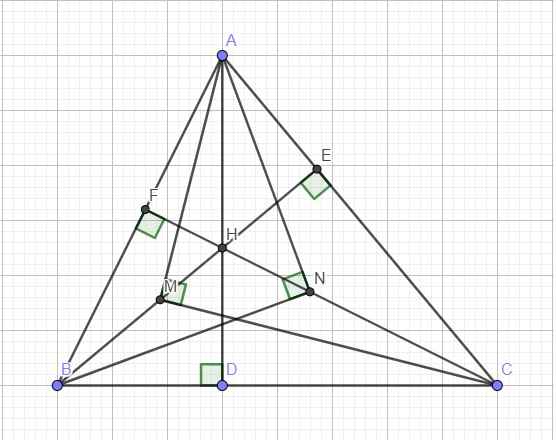
Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A


a) Xét tứ giác BIEM có
\(\widehat{IBM}\) và \(\widehat{IEM}\) là hai góc đối
\(\widehat{IBM}+\widehat{IEM}=180^0\)(\(90^0+90^0=180^0\))
Do đó: BIEM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔B,I,E,M cùng thuộc 1 đường tròn(đpcm)
b) Ta có: ABCD là hình vuông(gt)
nên BD là tia phân giác của \(\widehat{ABC}\)(Định lí hình vuông)
⇔BE là tia phân giác của \(\widehat{ABC}\)
⇔\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{IBE}=45^0\)
Ta có: BIEM là tứ giác nội tiếp(cmt)
nên \(\widehat{IBE}=\widehat{IME}\)(Định lí)
mà \(\widehat{IBE}=45^0\)(cmt)
nên \(\widehat{IME}=45^0\)
Vậy: \(\widehat{IME}=45^0\)