Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD là hình vuông (giả thiết).
\(\Rightarrow AB=BC=CD=DA\)(tính chất)
Và \(AB//CD\)(tính chất) \(\Rightarrow AB//DF\).
Và \(AD//CE\)(tính chất) \(\Rightarrow CE//AD\)
\(AB//DF\)(chứng minh trên)
\(\frac{AB}{AE}=\frac{FC}{FE}\)(hệ quả của định lí Ta-lét)
\(\Rightarrow\frac{AD}{AE}=\frac{FC}{FE}\)(vì \(AB=AD\))
\(\Rightarrow\frac{AD^2}{AE^2}=\frac{FC^2}{FE^2}\left(1\right)\)
Vì \(AB//CF\)(giả thiết)
\(\Rightarrow\frac{BE}{CE}=\frac{AE}{FE}\)(hệ quả của định lí Ta-lét) (2)
\(\Rightarrow\frac{BE}{CE+BE}=\frac{AE}{FE+AE}\)(tính chất của tỉ lệ thức)
\(\Rightarrow\frac{BE}{BC}=\frac{AE}{AF}\)\(\Rightarrow\frac{BE}{AD}=\frac{AE}{AF}\)(vì \(AD=BC\))
\(\Rightarrow\frac{AD}{AF}=\frac{BE}{AE}\)(tính chất của tỉ lệ thức)
Từ (2) \(\Rightarrow\frac{BE}{AE}=\frac{CE}{FE}\)(tính chất của tỉ lệ thức)
Do đó \(\frac{AD}{AF}=\frac{CE}{FE}\Rightarrow\frac{AD^2}{AF^2}=\frac{CE^2}{FE^2}\left(3\right)\)
Từ (1) và (3)
\(\Rightarrow\frac{AD^2}{AE^2}+\frac{AD^2}{AF^2}=\frac{FC^2}{FE^2}+\frac{CE^2}{FE^2}\)
\(\Rightarrow AD^2\left(\frac{1}{AE^2}+\frac{1}{AF^2}\right)=\frac{FC^2+CE^2}{FE^2}\)
Vì ABCD là hình vuông (giả thiết)
\(\Rightarrow BC\perp CD\)(tính chất)\(\Rightarrow EC\perp DF\)
Do đó \(\Delta CEF\)vuông tại C.
\(\Rightarrow CE^2+CF^2=EF^2\)(định lí Py-ta-go)
Do đó: \(AD^2\left(\frac{1}{AE^2}+\frac{1}{AF^2}\right)=\frac{FE^2}{FE^2}=1\)
\(\Rightarrow\frac{1}{AE^2}+\frac{1}{AF^2}=\frac{1}{AD^2}\)(điều phải chứng minh).

I don't now
...............
.................

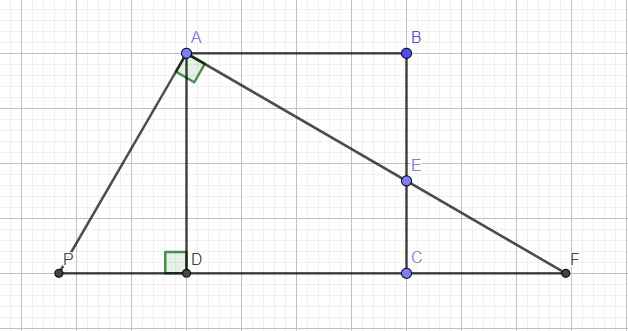
Qua A kẻ đường thẳng vuông góc AF cắt đường thẳng CD tại P
Xét hai tam giác vuông ABE và ADP có:
\(\left\{{}\begin{matrix}\widehat{B}=\widehat{D}=90^0\\AB=AD\\\widehat{BAE}=\widehat{DAP}\left(\text{ cùng phụ }\widehat{DAE}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta ADP\Rightarrow AP=AE\)
Áp dụng hệ thức lượng trong tam giác vuông APF:
\(\dfrac{1}{AD^2}=\dfrac{1}{AP^2}+\dfrac{1}{AF^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\) (đpcm)

bạn tự vẽ hình nha
qua A kẻ AI vuông góc với EF cắt BC tại I
áp dụng hệ thức lượng vào tam giác vuông AEI có AB là đường cao \(\frac{1}{AB^2}=\frac{1}{AE^2}+\frac{1}{AI^2}\) (1)
de dang chung minh duoc tam giac vuong ABI= tam giac vuong AFD(cgv-gnk)
\(\Rightarrow AF=AI\)
thay vao 1 ta co \(\frac{1}{AB^2}=\frac{1}{AE^2}+\frac{1}{AF^2}\left(DPCM\right)\)
qua A vẽ đường thẳng vuông góc với AE cắt CD tại G
xét tam giác ABE và tam giác ADG có
góc BAE = góc GAD ( vì cùng phụ với góc DAE )
AB=AD ( vì tứ giác ABCD là hình vuông )
góc ADG = góc ABE = 90 độ
=> tam giác ABE = tam giác ADG (g.c.g)
=> AE=AG => 1/AE^2=1/AG^2 (1)
mặt khác xét tam giác GAF vuông tại A có đường cao AD nên ta có
1/AG^2 + 1/AF^2 = 1/AD^2 (2)
từ (1) và (2) => 1/AD^2 = 1/AE^2 + 1/AF^2 mà AD = AB => 1/AB^2 = 1/AE^2 + 1/AF^2