Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chu vi hình vuông ABCD là :
3 * 4 = 12 ( cm )
Diện tích hình vuông ABCD là :
3 * 3 = 9 ( cm2 )
b) sai đề vì nối E với A thì mới ra hình thang, nếu không thì ra hình vuông với một cạnh kéo dài mà thôi

Mk nghĩ bn viết đề bài sai rùi, bn đã cho biết P ở đâu đâu mà đã cho BE=ED=PD

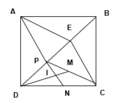
Vẽ hình đúng
a) Tính đúng diện tích hình vuông ABCD
b)-Lập luận đúng diện tích các tam giác ADP, APE, AEB, CPD, CPE, CEB bằng nhau và bằng 1 6 diện tích hình vuông ABCD.
-Lập luận được diện tích hình AECP bằng 1 3 diện tích hình vuông ABCD
-Tính đúng kết quả 12cm2
c)- Lập luận đúng diện tích tam giác DPM và DPN bằng nhau
- Lập luận đúng diện tích tam giác PMI và DNI bằng nhau

Bạn tham khảo nhé !
a) Nửa chu vi hay tổng chiều dài và chiều rộng của hình chữ nhật là:
60 : 2 = 30 (cm)
Chiều dài AB gấp rưỡi chiều rộng BC nghĩa là chiều dài bằng \(\frac{3}{2}\) chiều rộng
Chiều dài: |---|---|---|
Chiều rộng: |---|---|
Tổng số phần bằng nhau là:
3 + 2 = 5 (phần)
Chiều dài AB của hình chữ nhật có độ dài là:
30 : 5 × 3= 18 (cm)
Chiều rộng BC của hình chữ nhật là:
30−18 = 12 (cm)
Diện tích của hình chữ nhật ABCD là:
12 . 18 = 216 (cm2)
b) Ta có SEAB=SBCD
Vì:
- ΔEAB có chiều cao hạ từ E lên đáy AB bằng chiều cao BC của tam giác BCD hạ từ B lên đáy DC,
- đáy AB=DC
SABM=SDBM
Vì:
- chiều cao AB=DC
- chung đáy BM
Nên ta có: SEAB−SABM=SBCD−SDBM
Hay SMBE=SMCD
c) SABM =\(\frac{2}{3}\).SMAD
Vì:
- Đường cao AB bằng đường cao hạ từ đỉnh M của ΔMAD
- Đáy BM = \(\frac{2}{3}\)BC = \(\frac{2}{3}\)AD
Mà 2 tam giác này chung đáy AM nên suy ra chiều cao hạ từ đỉnh B lên AM của ΔMAB bằng \(\frac{2}{3}\) chiều cao hạ từ đỉnh D của ΔMAD lên đáy AM.
Đây cũng là chiều cao từ các đỉnh hạ lên đáy MO
ΔMBO và ΔMDO chung đáy MO
Chiều cao hạ từ B lên đáy MO của ΔMBO bằng \(\frac{2}{3}\)chiều cao hạ từ đỉnh DD lên đáy MO của ΔMDO
⇒\(\frac{SMBO}{SMOD}\) = \(\frac{2}{3}\)
ΔMBO và ΔMDO chung chiều cao hạ từ M lên BD
⇒\(\frac{OB}{OD}=\frac{2}{3}\)
k nha
đúng![]()
a) Nửa chu vi hay tổng chiều dài và chiều rộng của hình chữ nhật là:
(cm)
Chiều dài AB gấp rưỡi chiều rộng BC nghĩa là chiều dài bằng chiều rộng
Chiều dài: |---|---|---|
Chiều rộng: |---|---|
Tổng số phần bằng nhau là:
(phần)
Chiều dài AB của hình chữ nhật có độ dài là:
(cm)
Chiều rộng BC của hình chữ nhật là:
(cm)
Diện tích của hình chữ nhật ABCD là:
b) Ta có
Vì:
- có chiều cao hạ từ E lên đáy AB bằng chiều cao BC của tam giác BCD hạ từ B lên đáy DC,
- đáy AB=DC
Vì:
- chiều cao AB=DC
- chung đáy BM
Nên ta có:
Hay
c)
Vì:
- Đường cao AB bằng đường cao hạ từ đỉnh M của
- Đáy BM==AD
Mà 2 tam giác này chung đáy AM nên suy ra chiều cao hạ từ đỉnh B lên AM của bằng chiều cao hạ từ đỉnh D của lên đáy AM.
Đây cũng là chiều cao từ các đỉnh hạ lên đáy MO
và chung đáy MO
Chiều cao hạ từ B lên đáy MO của bằng chiều cao hạ từ đỉnh lên đáy MO của .
và chung chiều cao hạ từ M lên BD
.


a) Chu vi hình chữ nhật là :
\(\left(10+6\right)\times2=32\left(cm\right)\)
Do hình vuông có chu vi bằng chu vi hình chữ nhật ấy nên chu vi của hình vuông ABCD là 32 cm
Cạnh hình vuông là :
\(32\div4=8\left(cm\right)\)
b) Do M là điểm chính giữa cạnh AB nên \(AM=MB=\frac{AB}{2}=4\left(cm\right)\)
Ta có \(S_{\Delta ADM}=\frac{AD\times AM}{2}=\frac{8\times4}{2}=16\left(cm^2\right)\)
Do N là điểm chính giữa cạnh BC nên \(BN=NC=\frac{BC}{2}=4\left(cm\right)\)
\(S_{\Delta ABN}=\frac{AB\times BN}{2}=\frac{8\times4}{2}=16\left(cm^2\right)\)
Xét \(\Delta ABN\)và \(\Delta AMN\)có chung đường cao hạ từ N xuống cạnh đáy
Mà đáy AM của \(\Delta AMN\) \(=\frac{1}{2}\)đáy AB của \(\Delta ABN\)
\(\Rightarrow S_{\Delta AMN}=\frac{1}{2}S_{\Delta ABN}=\frac{1}{2}\times16=8\left(cm^2\right)\)
Kẻ \(NO\perp AD\)
Xét tứ giác ABNO có \(\widehat{OAB}=\widehat{ABN}=\widehat{NOA}=90^o\)
\(\Rightarrow\) ABNO là hình chữ nhật
\(\Rightarrow NO=AB=8\left(cm\right)\)
\(S_{\Delta AND}=\frac{NO\times AD}{2}=\frac{8\times8}{2}=32\left(cm^2\right)\)
Vậy ...