Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mk chỉ nêu cách làm bạn tự triển khai nha!
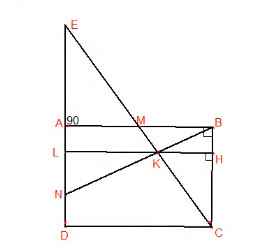
CM \(\Delta ADC=\Delta CBE (g.c.g)\) (*)
(\(\angle C_1=\angle C_2\) cùng phụ với \(\angle ACB\))
\(\Rightarrow AC=CE\Rightarrow \Delta ACE \) cân tại C
\(\Rightarrow AB=CE\)
Từ (*) suy ra:
\(S_{ANEC}=S_{ACE}+S_{ANE}=S_{ABCD}+S_{ANE}\)
\(=\dfrac{1}{2}AB^2+\dfrac{1}{2}NA.2AB=\dfrac{1}{2}AB(AB+2NA)\)
Mà \( S_{ANCE}=\dfrac{15}{8} S_{ABCD}\) \(\Rightarrow \dfrac{15}{8}.\dfrac{1}{2} AB^2=\dfrac{1}{2}.AB(2AN+AB)\)
\(\Rightarrow 2AN+AB=\dfrac{15}{8}AB\) \(\Rightarrow \dfrac{NA}{AB}=\dfrac{7}{16}\)
CM \(\Delta NAM \) đồng dạng với \(\Delta CBM\) \((g.g)\)
\(\Rightarrow \dfrac{NA}{AB}=\dfrac{NA}{BC}=\dfrac{AM}{MB}=\dfrac{7}{16}\)
Vậy cần lấy M sao cho \(\dfrac{AM}{MB}=\dfrac{7}{16}\)

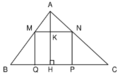
Vì ∆ ABC đồng dạng với ∆ AMN nên:
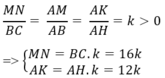
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
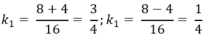
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
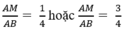

Vì ∆ ABC đồng dạng với ∆ AMN nên:
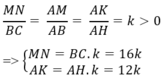
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
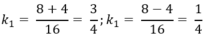
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
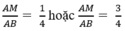

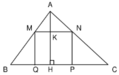
Gọi M, N, P lần lượt là trung điểm của EF, EG, HG
∆AEF vuông tại A có AM là trung tuyến nên AM = 1/2EF
∆HCG vuông tại C có CP là trung tuyến nên CP = 1/2GH
∆EFG có MN là đường trung bình nên MN = 1/2FG
∆EGH có NP là đường trung bình nên NP = 1/2EH
Chu vi tứ giác EFGH bằng EF + FG + GH + HE = 2(AM + MN + NP + PC) ≥ 2AC
Dấu "=" xảy ra khi A, M, N, P, C thẳng hàng theo thứ tự đó
<=> FG // AC // EH, EF // BD // HG <=> Tứ giác EFGH là hình bình hành
Cách xác định điểm: Lấy điểm F trên AB sao cho EF // BD, sau đó lần lượt lấy các điểm H, G trên CD, BC sao cho EH // AC // FG

Vì E thuộc cạnh AB nên EB < AB hay 2x < y
Ta có: AE = AB – EB = y – 2x (cm)
AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)
Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:
(y – 2x)(y + 3x) = y 2
Theo định lí Pitago, ta có: F C 2 = E B 2 + D G 2
Chu vi ngũ giác ABCFG:
PABCFG = AB + BC + CF + FG + GA
= AB + BC + CF + FG + GD + DA
= y + y + x 13 + y – 2x + 3x + y = x(1 + 13 ) + 4y
Vì chu vi ngũ giác ABCFG bằng 100 + 4 13 (cm) nên ta có phương trình:
x(1 + 13 ) + 4y = 100 + 4 13
Ta có hệ phương trình:
Giá trị của x và y thỏa điều kiện bài toán.
Vậy x = 4 (cm), y = 24 (cm).