Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương pháp: Tính góc giữa mặt phẳng (SAB) và (ABCD).
Cách giải: Dễ thấy 2 hình chóp S.ABCD và S’.ABCD là các hình chóp tứ giác đều.
Gọi E là trung điểm của AB ta có:
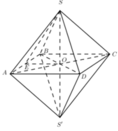
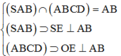
=> ((SAB);(ABCD)) = (SE;OE) = SEO = α
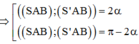
Ta có: 
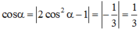

Đáp án A
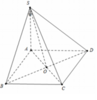
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .

Đáp án B

Vì ABCD là hình vuông ⇒ A B ⊥ A D 1
Ta có S A B ⊥ A B C D S A C ⊥ A B C D ⇒ S A ⊥ A B C D ⇒ S A ⊥ A B 2
Từ (1), (2) suy ra A B ⊥ S A D ⇒ S B ; S A D ^ = S B ; S A ^ = B S A ^
Tam giác SAB vuông tại A, có cos B S A ^ = S A S B = S A S A 2 + A B 2 = 2 5 5 .

Chọn B.
Phương pháp: Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.


Đáp án D
Phương pháp:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
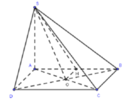
Gọi H là trung điểm của AB => OH//AD
ABCD là hình vuông => AD ⊥ AB; OH ⊥ AB
Mà OH ⊥ SA, (vì SA ⊥ (ABCD))
=> OH ⊥ (SAB)
=>SH là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
=> (SO,(SAB)) = (SO,SH) = HSO
Ta có: OH là đường trung bình của tam giác ABD 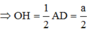
Tam giác SAH vuông tại A ![]()
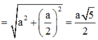
Tam giác SHO vuông tại H: 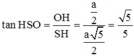

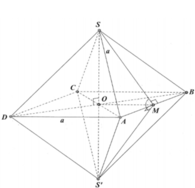
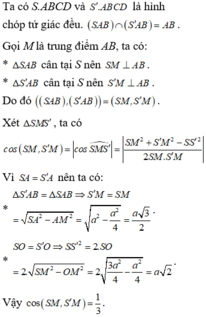
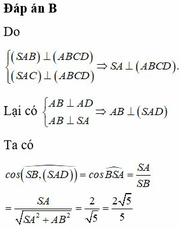

Chọn C