Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng nằm trên một đường tròn
b: Tâm là trung điểm của AC

a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
b: Tâm là trung điểm của AC
Bán kính là \(\dfrac{a\sqrt{2}}{2}\)

a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
\(R=\dfrac{AC}{2}\)

Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
Tâm là trung điểm của BD
Bán kính là một nửa của BD

a: \(DH=\dfrac{12^2}{16}=9\left(cm\right)\)
AB=căn 16*25=20(cm)
=>DC=20cm
AD=căn (25^2-20^2)=15cm
=>BC=15cm
b: Vì góc BAD+góc BCD=180 độ
nên ABCD là tứ giác nội tiếp
Bán kính là AC/2=20/2=10

Đáp án C
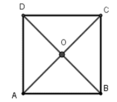
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
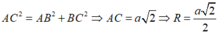
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là R = a 2 2

Chọn đáp án C
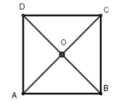
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
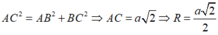
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là 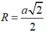

a: Xét tứ giác ABCD có
ˆA+ˆC=1800A^+C^=1800
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
R=AC2