Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: EA = EC
FB=FC
=> FC/EC=FB/EA Theo Talét đảo => AE//BF 2.C = 45 độ
=> ABC là tam giác vuông cân tại A
Xét tam giác vuông BAF có BF^2=BA^2+AF^2=5BA^2 (1)
Dễ thấy AD là đường cao tam giác vuông cân ABC nên AD = BD =AB /2
AE = BC = AB căn2, pitago vào tam giác vuông EDB
=> BE2 = 5AB2 (2)
Từ (1) và (2)suy ra BE=BF
Vậy vuông góc chứng minh BEF =45 độ
Giải :
Có EA=EC
FB=FC
SUY RA FC/EC=FB/EA
theo Talét đảo suy ra AE//BF
2.C = 45 độ suy ra ABC là tam giác vuông cân tại A
XÉT tam giác vuông BAF có BF^2=BA^2+AF^2=5BA^2 (1)
Dễ thấy AD là đường cao tam giác vuông cân ABC nên AD=BD=ABcăn2/2
AE=BC=ABcăn2, pitago vào tam giác vuông EDB suy ra BE^2=5AB^2 (2)
Từ (1) và (2)suy ra BE=BF
CÁi vuông góc chứng minh BEF =45 độ

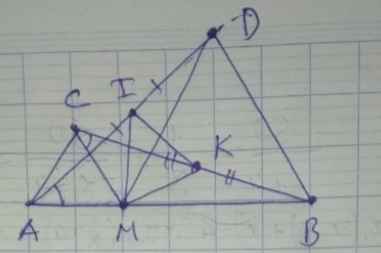
a) Ta có: \(\widehat{AMD}=\widehat{AMC}+\widehat{CMD}\)
\(=60^0+\widehat{CMD}\) \(\left(1\right)\)
Lại có: \(\widehat{CMB}=\widehat{BMD}+\widehat{CAD}\)
\(=60^0+\widehat{CMD}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\): ⇒ \(\widehat{AMD}=\widehat{CMB}\)
Xét △ AMD và △ CMB có:
CH = AM ( △ AMC đều )
\(\widehat{AMD}=\widehat{CMB}\) ( cmt )
MB = MD ( △ BMD đều )
⇒ △ AMD = △ CMB ( c - g - c )
Do đó: AD = CB ( 2 cạnh tương ứng )
b) Ta có: \(CK=\dfrac{BC}{2}\) ( K là trung điểm CB )
Ta có: \(AI=\dfrac{AD}{2}\) ( I là trung điểm AD )
Mà BC = AD ( cmt ) ⇒ CK = AI
Xét △ AMI và △ CMK có:
CM = AM ( △ AMC đều )
\(\widehat{IAM}=\widehat{KCM}\) ( vì △ AMD = △ CMB )
AI = CK ( cmt )
⇒ △ AMI = △ CMK ( c - g - c )
⇒ MK = MI
⇒ △ IMK cân tại M
Giải:
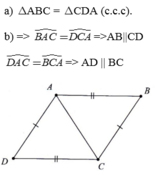
Xét \(\Delta ABC,\Delta ADC\) có:
\(\widehat{A_1}=\widehat{C_1}\) ( do đây là 2 góc so le trong và AB // CD )
\(AB=CD\left(gt\right)\)
\(\widehat{A_2}=\widehat{C_2}\) ( do đây là 2 góc so le trong và AB // CD )
\(\Rightarrow\Delta ABC=\Delta ADC\left(g-c-g\right)\)
\(\Rightarrow AD=BC\) ( cạnh tuong ứng )
Mà \(\widehat{A_2}=\widehat{C_2}\) ( do đây là góc so le trong và AB // CD ) và 2 góc này ở vị trí so le trong nên AD // BC
Vậy AD = BC; AD // BC