Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
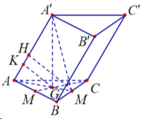
Gọi M,G lần lượt là trung điểm của BC và trọng tâm G của tam giác ABC.
Do tam giác ABC đều cạnh a nên 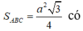
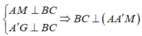
Trong mặt phẳng (AA'M) kẻ MH
⊥
AA'. Khi đó: ![]()
Vậy MH là đoạn vuông góc chung của AA' và BC nên MH = a 3 4 .
Trong tam giác AA'G kẻ ![]()
![]()
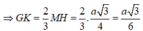
Xét tam giác AA'G vuông tại G ta có: ![]()

![]()
Vậy thể tích của khối lăng trụ đã cho là 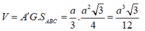

Đáp án A
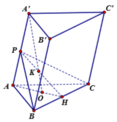
Gọi H là trung điểm của BC, giao điểm của (P) và A A ' là P.
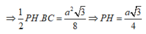

∆ A H P vuông tại P có A P = A H 2 - P H 2 = 3 a 4
∆ A A ' O ~ ∆ A H P ⇒ A ' O A O = H P A P
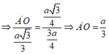
⇒ V A B C . A ' B ' C ' = O A ' . S A B C = a 3 3 12
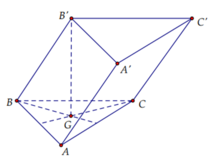
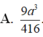
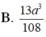
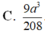
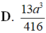
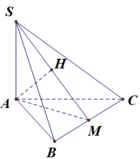

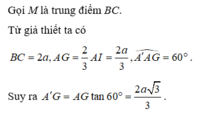
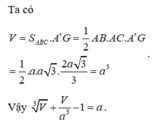
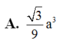
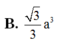
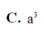


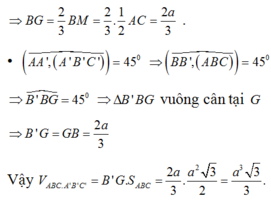
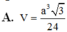

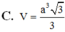
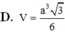
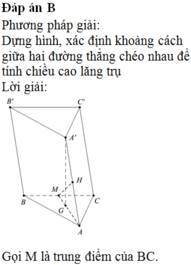
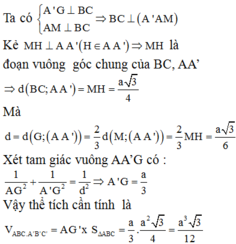
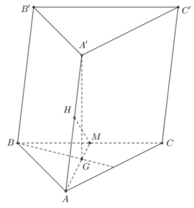

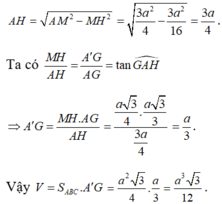
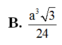

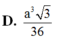
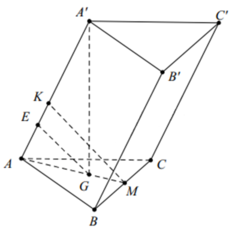

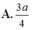

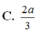
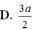

Góc giữa BB' và (ABC) là \(\widehat{B'BG}=60^0\). Suy ra đường cao \(B'G=BB'.\sin60^0=\dfrac{a\sqrt{3}}{2}\)
Lại có \(BG=BB'.\cos60^0=\dfrac{a}{2}\)
Gọi M là trung điểm AC thì \(BM=\dfrac{3}{2}BG=\dfrac{3a}{4}\)
Đặt AC=x thì \(BC=AC.\tan 60^0=x\sqrt{3}\)
Suy ra \(BM=\sqrt{BC^2+CM^2}=\sqrt{3x^2+\dfrac{x^2}{4}}=\dfrac{x\sqrt{13}}{2}=\dfrac{3a}{4}\). Suy ra \(x=\dfrac{3a\sqrt{13}}{26}\)
Do đó \(S_{ABC}=\dfrac{1}{2}BC.AC=\dfrac{x^2\sqrt{3}}{2}=\dfrac{9a^2\sqrt{3}}{52}\)
Vậy \(V_{A'ABC}=\dfrac{1}{3}BB'.S_{ABC}=\dfrac{3a^2\sqrt{3}}{52}\)
Gọi G là trong tâm tam giác ABC ta có B′G⊥(ABC)Từ đó B′BCG^=600 là góc mà B′B′ tạo với mặt phẳng (ABC). Trong tam giác vuông BB′G ta có ngay: BG=a2,B′G=a3√2BG=a2,B′G=a32
Đặt AB=2xAB=2x, trong tam giác vuông ABCABC ta có:
AC=x,BC=x3√AC=x,BC=x3 (do ABCˆ=600ABC^=600)
Giả sử BG∩ACBG∩AC thì BN=a2BG=3a4BN=a2BG=3a4.
Áp dụng định lí py ta go trong tam giác vuông BNCBNC ta có:
BN2=NC2+BC2⇒9a216=x24+3x2⇒x2=9a252(1)BN2=NC2+BC2⇒9a216=x24+3x2⇒x2=9a252(1)
ta có VA′ABC=13SABC.B′G=13.12.AB.BC.a3√2=a3√12x.x3√=ax24(2)VA′ABC=13SABC.B′G=13.12.AB.BC.a32=a312x.x3=ax24(2)
thay (2)(2) vào (1)(1) ta có: VA′.ABC=9a3208VA′.ABC=9a3208 (đvtt)