Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

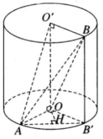
Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2

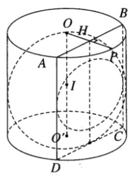
Vì các mặt đáy của hình trụ vuông góc với trục OO’ tại O và O’ nên chúng tiếp xúc với mặt cầu đường kính OO’.
Gọi I là trung điểm của đoạn OO’. Ta có I là tâm của mặt cầu. Kẻ IM vuông góc với một đường sinh nào đó (M nằm trên đường sinh) ta đều có IM = r là bán kính của mặt trụ đồng thời điểm M cũng thuộc mặt cầu. Vậy mặt cầu tiếp xúc với tất cả các đường sinh của mặt trụ.

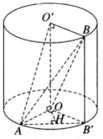
Vì trục OO’ vuông góc với các đáy nên OO′ ⊥ OA; OO′ ⊥ O′B. Vậy các tam giác AOO’ và BO’O vuông tại O và O’.
Theo giả thiết ta có AO ⊥ O′B mà AO ⊥ OO′ ⇒ AO ⊥ (OO′B). Do đó, AO ⊥ OB nên tam giác AOB vuông tại O. Tương tự, ta chứng minh được tam giác AO’B vuông tại O’. Thể tích hình chóp OABO’ là:
![]()
Hay
![]()

Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25
Gọi C C 1 và D D 1 là hai đường sinh của khối trụ
Khi đó D 1 C 1 / / = D C (1)
Đông thời ABCD là hình vuông nên AB//=DC (2)
Từ (1) và (2) suy ra AB//= D 1 C 1
Vậy A B C 1 D 1 nội tiếp đường tròn (O) nên A B C 1 D 1 là hình chữ nhật. Suy ra A C 1 là đường kính của (O)
Nghĩa là A C 1 = 2 r
Tam giác A B C 1 vuông ở B nên:
![]() (3)
(3)
Tam giác B C C 1 vuông ở C 1 nên:
![]() (4)
(4)
Từ (3) và (4) suy ra
![]()
Vậy diện tích hình vuông ABCD là S = A B 2 = 5 r 2 2
* Gọi α là góc hợp bởi mp(ABCD) và mặt phẳng đáy của hình trụ, ta có:
![]()
Với 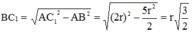
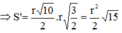
Mà A B C 1 D 1 là hình chiếu của ABCD trên mặt đáy hình trụ nên:
S
'
=
S
.
cos
α
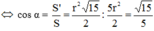


Do đó bán kính đường tròn \(\left(S\right)\cap\left(S'\right)\) bằng \(\dfrac{10\sqrt{41}}{41}a\)

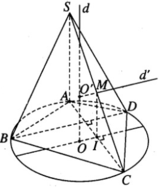
Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I. Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp. Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD. Ta có d ⊥ (ABCD) tại O. Gọi M là trung điểm của cạnh SC. Ta có MI // SA nên MI ⊥ (ABCD) tại I. Từ M kẻ đường thẳng d’ // OI cắt d tại O’. Vì d′ ⊥ (SAC) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có:
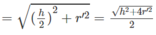



Hs lớp 12 không biết lên mạng tra xem có không rồi mới hỏi à.-.
Trên mạng nhiều khi không giải như cách chúng ta học đâu bạn, liệu thầy cô có biết và xem qua đáp án trên mạng không nhỉ? Không phải là có biết lên mạng tra hay không mà đã tra và muốn có 1 cách giải khác thôi ạ!