Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi hình thoi là $ABCD$ có $AC=12, BD=8$ (cm)
Trung điểm của $AB,AD,CD,CB$ lần lượt là $M,N,P,Q$
Dễ thấy:
$MQ, NP\parallel AC$ và $MQ=NP=\frac{AC}{2}=6$ (cm)
$NM, QP\parallel BD$ và $MN=QP=\frac{BD}{2}=4$ (cm)
Mà $BD\perp AC$ (tính chất hình thoi)
$\Rightarrow (MQ\parallel NP)\perp (MN\parallel QP)$
$\Rightarrow MNPQ$ là hình chữ nhật
$S_{MNPQ}=MN.NP=4.6=24$ (cm2)


Cho hình chữ nhật ABCD; M,N,P,Q lần lượt là trung điểm của AB,BC, CD, DA.
* Chứng minh MNPQ là hình thoi
Ta có MN = PQ = 1/2BD
NP = MQ = 1/2 AC
Mà AC = BD
⇒ MN = NP = PQ = QM nên tứ giác MNPQ là hình thoi (Có 4 cạnh bằng nhau)
* Theo bài 33 (các em tham khảo ở trên), ta có SMNPQ = SABNQ và SMNPQ = SNQDC
Vì vậy SABCD = SABNQ + SNQDC = 2SMNPQ
* Ta có SABCD =2SMNPQ ⇒ SMNPQ = 1/2SABCD = 1/2AB.BC = 1/2NQ.MP
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh M, N, P, Q.
Vẽ tứ giác MNPQ
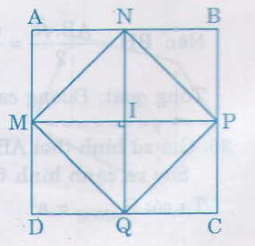
Ta có MN = PQ = \(\dfrac{1}{2}\)BD
NP = MQ = \(\dfrac{1}{2}\) AC
Mà AC = BD
Nên tứ giác MNPQ là hình thoi vì có bốn cạnh bằng nhau.
Dễ dàng chứng minh rằng : ∆AMN = ∆INM , ∆BPN = ∆NIP
∆PCQ = ∆IQP, ∆DMQ = IQM
Do đó
SMNPQ = \(\dfrac{1}{2}\) SABCD mà SABCD = AB. AD = MP. NQ
Vậy SMNPQ = \(\dfrac{1}{2}\) MP.NQ

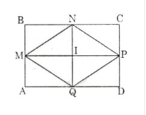
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh là M, N, P, Q.
Vẽ tứ giác MNPQ

Lại có: ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3) suy ra: MN = PQ = MQ = NP
=> Tứ giác MNPQ là hình thoi.
+ Ta có:
∆ BMN = ∆ IMN; ∆ INP = ∆ CNP, ∆ AMQ= ∆IMQ, ∆ DPQ= ∆IPQ
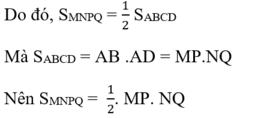
Như vậy diện tích hình thoi bằng nửa tích hai đường chéo.
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.