Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tứ giác AOBE có
IA=IB (gt)
IE=IO (gt)
=> AOBE là hbh (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường) (1)
Ta có \(AC\perp BD\) (Trong hình thoi hai đường chéo vuông góc với nhau) \(\Rightarrow\widehat{AOB}=90^o\) (2)
Từ (1) và (2) => AOBE là HCN (Hình bình hành có 1 góc bằng 90 thì là HCN)
b/
Ta có
OE=AB=5 cm (trong HCN hai đường chéo bằng nhau)
\(\Rightarrow C_{ABCD}=4.AB=4.5=20cm\)
c/
Ta có
EA//BO và EA=BO (trong hbh các cặp cạnh đối // và bằng nhau từng đôi một)
Mà BO=DO
=> EA=DO
mà \(DO\in BO\) nên EA//BO//DO
=> tứ giác AEOD là hbh (Tứ giác có cặp cạnh đối // và bằng nhau là hbh)
Nối ED cắt AO tại M' => M'A=M'O (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường) => M' là trung điểm của AO
Mà M cũng là trung điểm của AO => M trùng M' => E; M; D thẳng hàng
d/
Khi AOBE là hình vuông => AO=BO
Mà \(AO=\frac{AC}{2};BO=\frac{BD}{2}\)
=> AC=BD => ABCD là hình vuông (Hình thoi có 2 đường chéo bằng nhau là hình vuông)

a: Xét tứ giác OBIC có
M là trung điểm của OI
M là trung điểm của BC
Do đó OBIC là hình bình hành
mà \(\widehat{BOC}=90^0\)
nên OBIC là hình chữ nhật
b: ta có: OBIC là hình chữ nhật
nên OI=BC
mà BC=AB
nên OI=AB

Hình bạn tự vẽ nha
a) Chứng minh OBIC là hình chữ nhật
Vì I đối xứng với O qua M nên
MO = MI
Xét tứ giác OBIC có :
MO = MI (cmt)
MB = MC ( Vì M là tđ BC )
mà OI giao BC tại M
=)) OBIC là hình bình hành (1)
Lại có ABCD là hình thoi
mà 2 đường chéo AC và BD giao nhau tại O
=)) góc AOB = góc COB = 90O (2)
Từ (1) và (2) =)) OBIC là hình chữ nhật
b) CM AB = OI
Vì OBIC là hình chữ nhật
=) OC = BI
mà OC = AO ( Vì ABCD là hình thoi )
=) BI = AO (3)
Lại có OBIC là hình chữ nhật
=)) OC // BI
mà O thuộc AC ( do O là tđ của AC )
=)) AC // BI hay AO // BI (4)
Từ (3) và (4) =)) ABIO là hình bình hành
=)) AB = OI
c) SABIO = ??? cm2
Vì ABCD là hình thoi
có 2 đường chéo AC và BD giao nhau tại O
=) O là tđ của AC
O là tđ của BD
mà AC = 6 cm
=) AO = OC = 6 : 2 = 3 ( cm )
Lại có BD = 9 cm
=) BO = OD = 9 : 2 = 4,5 (cm )
Xét tam giác BOC ( góc BOC = 90O ) có :
BC2 = OB2 + OC2 ( Theo định lý Pitago )
=) BC = \(\sqrt{3^2+\left(4,5\right)^2}\)
=) BC \(\approx5,4\left(cm\right)\)
Lại có BM = MC = BC chia 2 =) BM = 2,7 ( cm )
Vì ABCD là hình thoi =) BC = AB = 5,4 cm
Vì OBIC là hình chữ nhật có
2 đường chéo OI và BC giao nhau tại M
=) \(BM\perp OI\)
Vì ABOI là hbh ( cmt câu b )
=) SABOI = AB . BM = 2,7 x 5,4 = 14 , 58 (cm2 )
Vậy ta có ĐPCM
Chúc bạn học tốt =)) ![]()

VÌ ABCD là hình thoi nên O là trung điểm của AC và BD
Suy ra: AC = 2OA = 2.3 = 6cm
Và BD = 2.OB = 2.5= 10cm
Diện tích hình thoi là:
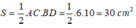
Chọn đáp án A

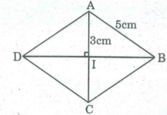
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: A B 2 = A I 2 + I B 2
⇒ I B 2 = A B 2 - A I 2 = 25 – 9 = 16
⇒ IB = 4(cm).
AC = 2AI = 2.3 = 6 (cm)
BD = 2IB = 2.4 = 8 (cm)
S A B C D = 1/2 AC.BD = 1/2 .6.8 = 24 ( c m 2 )

Chọn B