Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Câu 4: Cho tam giác ABC vuông tại A. Biết AB=5cm, BC=13cm. Gọi H, K lần Lượt là trung điểm của AB và BC. Tính độ dài HK
giúp mình nhoa!!

a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.


a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
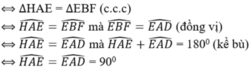
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.

Bài 1
a/Xét tứ giác BHCD có M đồng thời là trung điểm của cả HD và BC
Do đó BHCD là hình bình hành \(\Rightarrow BH//CD,CH//BD\)
Mặt khác vì ta có H là trực tâm của tam giác ABC nên \(BH\perp AC,CH\perp AB\)
Suy ra \(BD\perp AB,CD\perp AC\Rightarrow\Delta ABD,\Delta ACD\)là tam giác vuông
b/Xét \(\Delta ABD,\Delta ACD:\widehat{ABD}=\widehat{ACD}=90^0\);I là trung điểm của cạnh huyền chung AD
Suy ra \(IA=IB=IC=ID\)
Bài 2a/Vì AD=CD(gt) nên D nằm trên trung trực của đoạn AC suy ra \(\widehat{DAC}=\widehat{ECA}=90^0-60^0=30^0\)
Suy ra \(\widehat{BAD}=90^0+\widehat{DAC}=120^0\)
b/Trước hết ta thấy ABCD đã là hình thang,nên ta đi chứng minh \(\widehat{BCD}=\widehat{ABC}=60^0\)
Ta có \(\widehat{BCD}=\widehat{DCA}+\widehat{ACB}=\widehat{DAC}+30^0=30^0+30^0=60^0\)
Vậy ABCD là hình thang cân
c/Ta có \(\Delta BCE:AE=BE,\widehat{ABE}=60^0\Rightarrow AE=BE=AB\)
\(\widehat{ADE}=\frac{1}{2}.\widehat{ADC}=60^0;\widehat{BAD}=120^0=\widehat{BED}\)
Suy ra ABED là hình bình hành
Mà ta còn có AB=EB
Vậy ABED là hình thoi
bạn tự vẽ hình theo giả thiết nha
a) xét hình thoi ABCD có:
góc B = góc C(t/c hình thoi)
góc A=góc C(t/c hình thoi)
mà góc B = 60 độ(gt)
=>góc C=60 độ
góc A+góc B+góc C+góc D=360 (độ)
thay góc B và góc C=60 độ(cmt)
=>góc A+60 (độ)+góc C+60(độ)=360(độ)
góc A+ góc C= 240(độ)
mà góc A=góc C(cmt)
=>2góc A= 240/2=120(độ)
Xét tứ giác ABKD có
góc BCD+góc DCK=180(độ)(kề bù)
=>góc DCK=180-góc BCD
góc BCD=120 độ (cmt)
=>góc DCK=60 độxét tam CDKBC=CK(gt)mà BC=CD(t/c hình thoi)=>CK=CD(t/c bắc cầu)=>tam CDK là tam cânmà tam cân có một góc=60 độ thì tam CDK là tam đều =>góc K= 60 độ=>góc B= góc C(=60 độ)(1)mà trong hình thoi ABCD có BC//AC(t/c hình thoi)mà điểm K nằm trên tia đốiBC=>BC và CK nằm trên một đường thẳng=>AD//BK=>ADKB là hình thang(dấu hiệu nhận biết hình thang(2)từ (1)(2)=>ABKD là hình thang cân (dấu hiệu nhận biết hình thang cân)b) xét hình thoi ABCD kẻ đường thẳng BC =>BC là đường chéo hình thoi ABCD=>góc ADB=góc BDC(t/c đường chóe hình thoi)=>góc BDC=gócADC/2=30 độgóc BDC +góc CDK= góc BDK=>30(độ)+60(độ)=90(độ)do BDC =30(độ)(cmt)góc CDK=60 độ(cmt)=>góc D = 90 độ=>BD vuông góc DKbạn xem thử có thiếu dữ kiện ở câu c không nha