Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



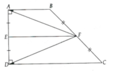
Gọi giao điểm của AF và DC là I.
\(\widehat{A}=\widehat{D}=90^0\Rightarrow AB//CD\Rightarrow\hept{\begin{cases}\widehat{ABF}=\widehat{ICF}\\\widehat{BAF}=\widehat{I}\left(1\right)\end{cases}\left(SLT\right)}\)
\(\Delta ABF=\Delta ICF\left(g.c.g\right)\Rightarrow AF=IF\)mà \(F\in AI\Rightarrow\) F là trung điểm của AI
Tam giác ADI vuông tại D có DF là đường trung tuyến ứng với cạnh huyền AI
\(\Rightarrow DF=\frac{1}{2}AI\Rightarrow DF=IF\Rightarrow\Delta IDF\)cân tại F \(\Rightarrow\widehat{FDC}=\widehat{I}\left(2\right)\) (t/c)
Từ (1) và (2), \(\widehat{BAF}=\widehat{CDF}\)
Chúc bạn học tốt.

a) Ta có È là đường trung bình của hình thang ABCD.
Þ EF//AB.
Suy ra EF ^ AD
Khi đó EF vừa trung tuyến, vừa là đường cao của tam giác AFD Þ ĐPCM.
b) Tam giác AFD cân tại F nên E A F ^ = E D F ^
Suy ra F A B ^ = C D F ^