Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
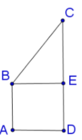
Ta có: A E = B F = 1
Khi đó: D E = A D 2 − A E 2 = 1
Khi quay hình chữ nhật DEFC quanh trục AB ta được hình trụ có thể tích là:
V 1 = π D E 2 . D C = π .1 2 .3 = 3 π
Khi quay tam giác AED quanh trục AB ta được hình nón có thể tích là:
V 2 = 1 3 π D E 2 . A E = 1 3 π .1 2 .1 = π 3
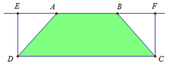
Do đó thể tích vận tròn xoay tạo thành khi cho hình thang quay quanh AB là:
V = V 1 − 2 V 2 = 7 π 3

Chọn đáp án C
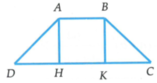
Gọi H, K lần lượt là hình chiếu của A và B trên cạnh CD.
Suy ra ABHK là hình chữ nhật và AB =HK = 1
![]()
Quay hình thang ABCD quanh cạnh AB, ta được một khối tròn xoay có thể tích là V = V 1 - 2 V 2 Trong đó:
+ V1 là thể tích của khối trụ có bán kính đáy r =AH =1 chiều cao h =CD =3
Ta có V = V 1 - 2 V 2 (đvtt).
+ V2 là thể tích của khối nón có bán kính đáy r =AH -1; chiều cao h ' = D H = 1
Ta có V 2 = 1 3 πr 2 h ' = 1 3 π đvtt (đvtt).
Vậy thể tích khối tròn xoay cần tính là V = 3 π - 2 . 1 3 π = 7 3 π (đvtt)

Đáp án D
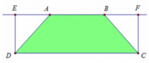
Ta có A E = B F = 1 Khi đó D E = A D 2 − A E 2 = 1
Khi quay hình chữ nhật DEFC quay trục AB ta được hình trụ có thể tích là: V 1 = π . D E 2 . D C = π 1 2 .3 = 3 π
Khi quay tam giác AED quanh trục AB ta được hình nón
có thể tích là V 2 = 1 3 π . D E 2 . A E = 1 3 π .1 2 .1 = π 3 . Do đó thể tích vật tròn xoay tạo thành khi cho hình thang đó quay quanh AB là: V = V 1 − 2 V 2 = 7 π 3 .

Đáp án B
Khi quay hình thang quanh AB, ta được khối tròn quay có thể tích băng thể tích hình trụ bán kính đáy AD, chiều cao CD trừ đi thể tích hình nón có bán kính đáy AD, chiều cao CE.
Dễ dàng tính được CE=1.
Ta có
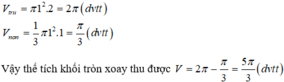

Đáp án A
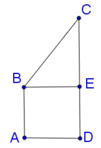
Khi quay hình thang quanh AB , ta được khối tròn quay có thể tích băng thể tích hình trụ bán kính đáy AD , chiều cao CD trừ đi thể tích hình nón có bán kính đáy AD , chiều cao CE.
Dễ dàng tính được CE=1.
Ta có


Đáp án D
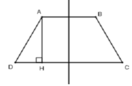
Khi quay hình thang cân ABCD quanh trục đối xứng ta được hình nón cụt có chiều cao h = 2 a 2 và bán kính 2 đáy là R 1 = a , R 2 = 2 a .
Vậy thể tích cần tính là V = πh 3 R 1 2 + R 2 2 + R 1 R 2 = 14 2 3 πa 3

Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
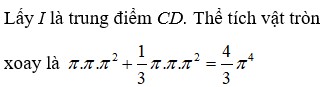

Chọn đáp án D