Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2:
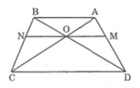
Xét ΔADC có OM//DC
nen OM/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thag ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1) (2)và (3) suy ra OM=ON
Bài 2:
Xét ΔADC có OM//DC
nen OM/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thag ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1) (2)và (3) suy ra OM=ON
Bài 2:
Xét ΔADC có OM//DC
nen OM/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thag ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1) (2)và (3) suy ra OM=ON
Trong ΔDAB, ta có: OM // AB (gt)
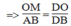(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
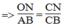(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: 
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: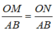 
Vậy: OM = ON
c. -Xét △ADC có: OM//DC (gt).
\(\Rightarrow\dfrac{MO}{DC}=\dfrac{AO}{AC}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{MO}=\dfrac{AC}{AO}\)
\(\Rightarrow\dfrac{DC}{OM}-1=\dfrac{OC}{AO}\) (1).
-Xét △BDC có: ON//DC (gt).
\(\Rightarrow\dfrac{ON}{DC}=\dfrac{BO}{BD}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{ON}=\dfrac{BD}{BO}\)
\(\Rightarrow\dfrac{DC}{ON}-1=\dfrac{OD}{BO}\)
-Xét △ABO có: AB//DC (gt).
\(\Rightarrow\dfrac{OD}{BO}=\dfrac{OC}{OA}=\dfrac{DC}{AB}\) (3)
-Từ (1), (2),(3) suy ra:
\(\dfrac{DC}{OM}-1=\dfrac{DC}{ON}-1=\dfrac{DC}{AB}\)
\(\Rightarrow\dfrac{DC}{OM}=\dfrac{DC}{ON}=\dfrac{DC}{AB}+1=\dfrac{AB+DC}{AB}\)
\(\Rightarrow\dfrac{1}{OM}=\dfrac{1}{ON}=\dfrac{AB+DC}{AB.DC}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
a: Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔAOB∼ΔCOD
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)
hay \(OA\cdot OD=OB\cdot OC\)
b: \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\)
\(\Leftrightarrow OA=\dfrac{1}{2}\cdot6=3\left(cm\right)\)
