Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có BI//AC gt / CI//BD BOC=90 độ (tcht) suy ra tứ giác OBIC LÀ hình chữ nhật dkpcm
có OBIC là hình chữ nhật suy ra OI=BC (tchcn) mà BC = AB suy ra OIBAB dkpcm
hình thoi abcd cần có 1 góc vuông hình chữ nhất OIBAB là hình vuông

A) xét tứ giác OCKB :có BK song song với OC( vì BK song song với AC)
: có CK song song với OB ( vì CK song song vớiOB)
Từ hai điều kiện trên ta kết luận tứ giác OCKB là hình bình hành
mà ta lạ có góc COB=90 độ
vậy tứ giác OCKC là hình chữ nhật
B) Ta có : BK song song với OA ( vì BK song song song với AC)
Hơn nữa BK lại bằng OC ( vì OCBK là hình chữ nhật)
Mà OC lại bằng OA suy ra BK=OA
từ những điều kiện trên suy ra tứ giác ABKO là HBH
vậy AB=OK
C)nếu cần tìm điều kiện ở tứ giác ABCD để thỏa mãn tứ giác OBKC là hình vuông thì ta sẽ chọn điều kiện đó là
tứ giác ABCD là hình vuông

a) tứ giác OBKC có BK // AC (GT) hay BK // OC
CK // BD (gt) hay CK // BO
=> OBKC là HBH ( vì là tứ giác có các cạnh đối //)
^BOC = 90ĐỘ (T/C Hthoi)
=> OBKC là HCN (vì là HBH có 1 góc vuông)
b) OBKC là HCN => OK = BC (t/c HCN) (1)
ABCD là Hthoi (gt) => AB = BC (t/c Hthoi) (2)
từ (1) và (2) => OK = AB
c) Hthoi ABCD cần ĐK ^A = 90ĐỘ để OBKC là Hvuông

a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
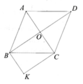

Đây chỉ là hướng giải, ko phải bài giải nhé ^^!
a) Chứng minh theo dấu hiệu hình hình hành có 1 góc vuông là hcn
b) Cm theo DH Tứ giác có 2 cạnh đối song song và bằng nhau là hình bình hành => AB = OI (2 cạnh đối)
c) Để OBIC là hình vuông thì OB = OC hay BD = AC <=> ABCD là hình vuông

a: Xét tứ giác DBKC có DB//KC
nên DBKC là hình thang
mà \(\widehat{OBK}=90^0\)
nên DBKC là hình thang vuông
b: Xét tứ giác OBKC có
OB//KC
OC//BK
Do đó: OBKC là hình bình hành
mà \(\widehat{BOC}=90^0\)
nên OBKC là hình chữ nhật
Suy ra: OK=BC
=>OK=AB