Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

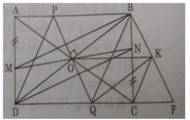
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.

Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
mình nghĩ là đề bài này bị sai hay sao đó, vì theo đề bài thì điểm M sẽ trùng với điểm I ( AD và BC đều vuông góc tại M và I ) . bạn có thể thử sửa đề thành : " qua N kẻ đường thẳng vuông góc với AD ,cắt đường thẳng M vuông góc với BC tại I " ( mình không chắc lắm nhưng mà bạn có thể thử .
Ok
mình sửa